题目内容
已知a+b=0,且|a-b|=
,则a2+ab-b2= .
| 2 |
| 3 |
考点:代数式求值
专题:
分析:根据已知求出b的值,把a+b=0和b=±
代入求出即可.
| 1 |
| 3 |
解答:解:∵a+b=0,
∴a=-b,
∵|a-b|=
,
∴|-2b|=
,
解得:b=±
,
∴a2+ab-b2
=a(a+b)-b2
=a×0-b2
=-b2
=-(±
)2
=-
,
故答案为:-
.
∴a=-b,
∵|a-b|=
| 2 |
| 3 |
∴|-2b|=
| 2 |
| 3 |
解得:b=±
| 1 |
| 3 |
∴a2+ab-b2
=a(a+b)-b2
=a×0-b2
=-b2
=-(±
| 1 |
| 3 |
=-
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题考查了绝对值,相反数,求代数式的值的应用,解此题的关键是求出b的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
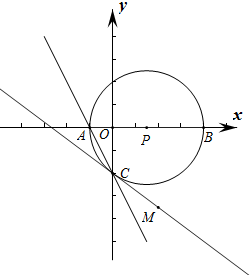 如图,在直角坐标中,坐标原点为O,A点的坐标为(-1,0),B点的坐标为(4,0),以AB的中点P为圆心作⊙P与y轴的负半轴交于点C.
如图,在直角坐标中,坐标原点为O,A点的坐标为(-1,0),B点的坐标为(4,0),以AB的中点P为圆心作⊙P与y轴的负半轴交于点C. 如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△DEA旋转一定角度后能与△DFA重合.
如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△DEA旋转一定角度后能与△DFA重合.