题目内容
14.已知,在△ABC中,BC=48cm,高AD=16cm,它的内接矩形MNPQ的一边NP落在BC边上,M,Q分别落在AB,AC上,又矩形MNPQ的两邻边之比为5:9,求此矩形的周长.分析 根据矩形的性质得到MQ∥BC,推出△AMQ∽△ABC,设MQ=5x,MN=9x,则AH=AD-HD=16-9x,根据相似三角形的性质得到$\frac{MQ}{BC}=\frac{AH}{AD}$,于是求得MQ=$\frac{15}{2}$,MN=$\frac{27}{2}$,求出矩形的周长=2(MQ+MN)=42(cm),当MQ=9x,MN=5x,则AH=AD-HD=16-5x,求得MQ=18,MN=10于是得到矩形的周长=2(MQ+MN)=56(cm),
解答 解: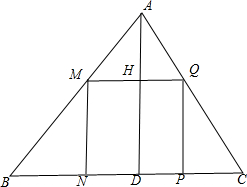 ∵矩形MNPQ,
∵矩形MNPQ,
∴MQ∥BC,
∴△AMQ∽△ABC,
设MQ=5x,MN=9x,则AH=AD-HD=16-9x,
∴$\frac{MQ}{BC}=\frac{AH}{AD}$,
∴$\frac{5x}{48}=\frac{16-9x}{16}$,
解得:x=$\frac{3}{2}$,
∴MQ=$\frac{15}{2}$,MN=$\frac{27}{2}$,
∴矩形的周长=2(MQ+MN)=42(cm),
当MQ=9x,MN=5x,则AH=AD-HD=16-5x,
∴$\frac{9x}{48}=\frac{16-5x}{16}$,
解得:x=2,
∴MQ=18,MN=10
∴矩形的周长=2(MQ+MN)=56(cm),
综上所述:矩形的周长为:42(cm)或56(cm).
点评 本题主要考查了勾股定理、矩形的性质及直角三角形的性质,熟练运用矩形的性质,及作出直角三角形斜边上的高,是解答本题的关键.

练习册系列答案
相关题目
19.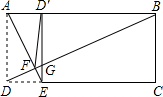 如图,在矩形ABCD中,AD=3.5,tan∠ABD=$\frac{2}{5}$,连接BD,E是CD上一点,连接AE,交BD于点F,将矩形ABCD沿AE折叠,点D恰好落在边AC的点D′处,则△EFD′的面积为( )
如图,在矩形ABCD中,AD=3.5,tan∠ABD=$\frac{2}{5}$,连接BD,E是CD上一点,连接AE,交BD于点F,将矩形ABCD沿AE折叠,点D恰好落在边AC的点D′处,则△EFD′的面积为( )
 如图,在矩形ABCD中,AD=3.5,tan∠ABD=$\frac{2}{5}$,连接BD,E是CD上一点,连接AE,交BD于点F,将矩形ABCD沿AE折叠,点D恰好落在边AC的点D′处,则△EFD′的面积为( )
如图,在矩形ABCD中,AD=3.5,tan∠ABD=$\frac{2}{5}$,连接BD,E是CD上一点,连接AE,交BD于点F,将矩形ABCD沿AE折叠,点D恰好落在边AC的点D′处,则△EFD′的面积为( )| A. | 1.75 | B. | 3 | C. | 3.5 | D. | 4 |
3.-(-1)3=( )
| A. | -3 | B. | -1 | C. | 3 | D. | 1 |

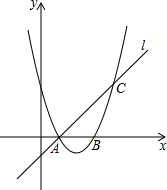 如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点的坐标是(4,3).
如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点的坐标是(4,3).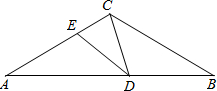 如图,△ABC中,BC=AC=4,∠ACB=120°,点E是AC上一个动点(点E与A,C不重合),ED∥BC,求S△CED的最大值.
如图,△ABC中,BC=AC=4,∠ACB=120°,点E是AC上一个动点(点E与A,C不重合),ED∥BC,求S△CED的最大值.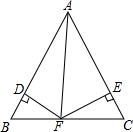 已知如图,△ABC为等边三角形,边长为a,点F是BC上任意一点,DF⊥AB,EF⊥AC
已知如图,△ABC为等边三角形,边长为a,点F是BC上任意一点,DF⊥AB,EF⊥AC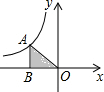 如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于B,若S△AOB=2,则这个反比例函数的解析式为y=-$\frac{4}{x}$.
如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于B,若S△AOB=2,则这个反比例函数的解析式为y=-$\frac{4}{x}$.