题目内容
【题目】已知等腰三角形ABC的三个顶点都在直径为10的⊙O上,如果圆心O到BC的距离为3,那么三角形ABC的面积为_________.
【答案】8或32或30.72(![]() )
)
【解析】
此题分情况考虑:①当BC是底边,△ABC是锐角三角形时;②当BC是底边,△ABC是钝角三角形时;③当BC是腰时;分别根据勾股定理和垂径定理求出等腰三角形的底边长和底边上的高,根据三角形的面积公式即可得到结论.
解:分情况讨论:
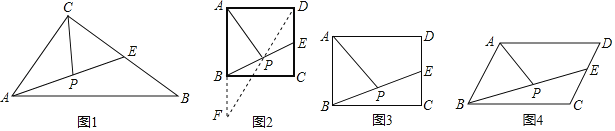
①当BC是底边,△ABC是锐角三角形时,连接AO并延长到BC于点D,如图1,
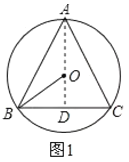
∵AB=AC,O为外心,
∴AD⊥BC,
在Rt△BOD中,OB=5,OD=3,
∴BD=![]() ,
,
∴AD=5+3=8,BC=2BD=8,
∴三角形ABC的面积=![]() ×8×8=32;
×8×8=32;
②当BC是底边,△ABC是钝角三角形时,连接AO交BC于点D,如图2所示,
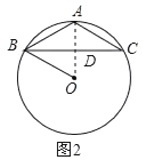
在Rt△BOD中,OB=5,OD=3,
∴BD=![]() ,
,
∴AD=53=2,BC=2BD=8,
∴三角形ABC的面积=![]() ×2×8=8,
×2×8=8,
③当BC是腰时,连接BO并延长到AC于点E,作OD⊥BC于点D,如图3所示,
在Rt△BOD中,OB=5,OD=3,
∴BD=![]() ,
,
∴BC=2BD=8,
设OE=x,
在Rt△COE中,![]() ,
,
在Rt△BCE中,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∴三角形ABC的面积=![]() ,
,

故答案为:8或32或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
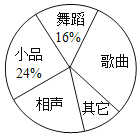
小学生10分钟应用题系列答案【题目】某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:
最喜爱的节目 | 人数 |
歌曲 | 15 |
舞蹈 | a |
小品 | 12 |
相声 | 10 |
其它 | b |
(1)在此次调查中,该校一共调查了 名学生;
(2)a= ;b= ;
(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;
(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.