题目内容
已知a2+ab-b2=0,且a,b均为正数,先化简下面的代数式,再求值: .
.
解:∵
=
= ,
,
解法一:∵a2+ab-b2=0,
∴ ,
,
∵a,b均为正数,
∴只取a= b,∴2a=(
b,∴2a=( -1)b,
-1)b,
∴原式= ;
;
解法二:∵a2+ab-b2=0,且a,b均为正数,
∴( )2+(
)2+( )-1=0,∴
)-1=0,∴ =
=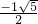 (负值舍去),
(负值舍去),
∴ ,
,
∴原式= .
.
分析:欲求值,但a、b的具体值未知,故化简后也不能直接代入.可以把a2+ab-b2=0看成是关于a的一元二次方程,用公式法求得 .又因为a,b均为正数,所以只取a=
.又因为a,b均为正数,所以只取a= b,即2a=(
b,即2a=( -1)b.最后可以采取整体代换的方法求值.
-1)b.最后可以采取整体代换的方法求值.
点评:本题为分式的化简求值题,但难点却在求a的值上,需要灵活运用公式法解一元二次方程.

=

=
 ,
,解法一:∵a2+ab-b2=0,
∴
 ,
,∵a,b均为正数,
∴只取a=
 b,∴2a=(
b,∴2a=( -1)b,
-1)b,∴原式=
 ;
;解法二:∵a2+ab-b2=0,且a,b均为正数,
∴(
 )2+(
)2+( )-1=0,∴
)-1=0,∴ =
=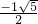 (负值舍去),
(负值舍去),∴
 ,
,∴原式=
 .
.分析:欲求值,但a、b的具体值未知,故化简后也不能直接代入.可以把a2+ab-b2=0看成是关于a的一元二次方程,用公式法求得
 .又因为a,b均为正数,所以只取a=
.又因为a,b均为正数,所以只取a= b,即2a=(
b,即2a=( -1)b.最后可以采取整体代换的方法求值.
-1)b.最后可以采取整体代换的方法求值.点评:本题为分式的化简求值题,但难点却在求a的值上,需要灵活运用公式法解一元二次方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. .
. .
.