Question

【题目】将等腰三角形折叠，使顶点与底边的中点重合，折线分别交、于点、，连接、．

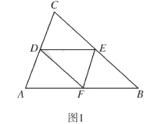
（1）如图1，求证：四边形是菱形；

（2）如图2，延长至点，使，连接，并延长交的延长线于点，在不添加任何辅助线的情况下，请直接写出图2中的所有平行四边形（不包括以为一边的平行四边形）

Answer 1

【答案】（1）见解析；（2）；；；；

【解析】

（1）连接BD，交EF于点O，利用已知条件和折叠的性质证明BE=BF和EF与BD垂直平分，即可证明四边形DFBE是菱形；
（2）根据平行四边形的各种判定方法即可直接写出图2中的所有平行四边形．

解：证明：（1）如图1，连接，交于点，

∵，点是的中点，

∴，，

由折叠可知，，

∴，

∴，

∴与垂直平分，

∴四边形是菱形；

（2）由（1）以及构图过程可知：

图2中共有五个平行四边形（不包括以为一边的平行四边形）．

分别是；；；；.