Question

【题目】等腰△ABC 中，AB＝AC，∠BAC＝120°，点 P 为平面内一点．

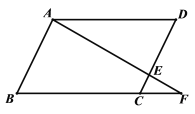
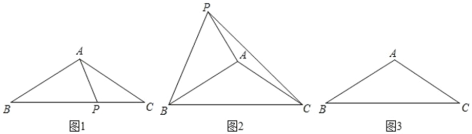
(1)如图 1，当点 P 在边 BC 上时，且满足∠APC＝120°，求的值；

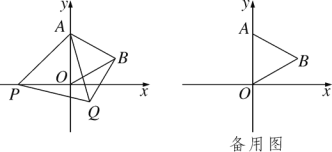
(2)如图 2，当点 P 在△ABC 的外部，且满足∠APC+∠BPC＝90°，求证：BP＝AP；

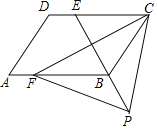
(3)如图 3，点 P 满足∠APC＝60°，连接 BP，若 AP＝1，PC＝3，直接写出BP 的长度．

Answer 1

【答案】(1)2;(2)见解析;(3) 2或．

【解析】

（1）由∠BAC＝120°，AB＝AC，推出∠B＝∠C＝30°，由∠APC＝120°，推出∠PAC＝∠C＝30°，推出PC＝PA，∠PAB＝90°，推出PB＝2PA，可得 PB＝2PC解决问题；

如图 2中，将线段AP绕点 A顺时针旋转120°得到线段AF，连接PF， BF，BF交 PC于点 H．想办法证明PB＝PF即可解决问题；

（3）分两种情形分别求解即可解决问题.

（1）如图1中，∵∠BAC＝120°，AB＝AC，

∴∠B＝∠C＝30°，

∵∠APC＝120°，

∴∠PAC＝∠C＝30°，

∴PC＝PA，∠PAB＝90°，

∴PB＝2PA，

∴PB＝2PC，

∴＝2；

(2)如图2中，将线段AP绕点A顺时针旋转120°得到线段AF，连接PF，BF，BF交PC于点H，

∵∠BAC＝∠PAF＝120°，

∴∠PAC＝∠BAF，

∵AB＝AC，AF＝AP，

∴△ABF≌△ACP（SAS），

∠APC＝∠AFB，

设∠APC＝α，则∠AFB＝α，∠PFB＝30°+α，∠BPC＝90°﹣α

∵∠PHB＝∠HPF+∠PFH＝（30°﹣α）+（30°+α）＝60°，

∴∠PBH＝180°﹣（90°﹣α﹣60°）＝30°+α，

∴∠PBF＝∠PFB，

∴PB＝PF，

在△PAF中，易知PF＝PA，

∴PB＝PA；

（3）①如图3﹣1中，当点P在△ABC外部时，将线段AP绕点A顺时针旋转 120°得到线段AF，连接PF，BF，

则△ABF≌△ACP（SAS），

∴∠AFB＝∠APC＝60°，BF＝PC＝3，

∵∠AFP＝30°，

∴∠BFP＝90°，

∵PA＝AF＝1，∠PAF＝120°，

∴PF＝，

∴PB＝＝2；

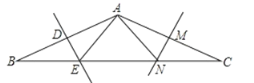
②如图3﹣2中，当点P在△ABC内部时，将线段AP绕点A逆时针旋转120° 得到AH，连接PH，HC．作HM⊥PC于M，

则△BAP≌△CAH（SAS），

∴PB＝CH，

∵∠PAH+∠APC＝120°+60°＝180°，

∴AH∥PC，

∴∠AHP＝∠HPM＝30°，

∴HM＝PH＝，

∴PM＝HM＝，

∵PC＝3，

∴CM＝PM＝，

∵HM⊥PC，

∴HC＝PH＝ ，

∴PB＝，

综上所述，满足条件的 PB 的值为 2或．