题目内容
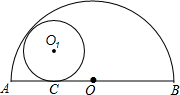 如图,半圆O的直径AB=4,与半圆内切的⊙O1与AB切于C,设AC=x,⊙O1的半径为y,则y与x的关系式为________.
如图,半圆O的直径AB=4,与半圆内切的⊙O1与AB切于C,设AC=x,⊙O1的半径为y,则y与x的关系式为________.
y=- x2+x
x2+x
分析:连接O1C,O1O,如图所示,由圆O1与AB相切,根据切线的性质得到O1C⊥AB,O1C为半径y,再由半圆直径AB的长,求出半径OA的长,用OA-AC及AC=x,表示出OC的长,由两圆内切,得到圆心距等于两半径之差,由大圆的半径2与小圆半径y之差表示出O1O,在直角三角形O1CO中,利用勾股定理列出关系式,将各自的值代入,化简后即可得到y与x的关系式.
解答:连接O1C,O1O,如图所示:
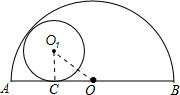
∵圆O1与AB相切与点C,且圆O1的半径为y,
∴O1C⊥AB,O1C=y,
∵AB=4,
∴OA=2,又AC=x,
∴OC=OA-AC=2-x,
∵圆O1与圆O内切,
∴圆心距d=OO1=2-y,
在Rt△O1CO中,根据勾股定理得:O1C2+CO2=O1O2,
即y2+(2-x)2=(2-y)2,
化简得:y=- x2+x.
x2+x.
故答案为:y=- x2+x
x2+x
点评:此题考查了两圆相切的性质,切线的性质,以及勾股定理,利用了数形结合的思想,当两圆外切时,圆心角等于两半径之和;当两圆内切时,圆心距等于两半径之差,解本题的关键是连接圆心与切点,构造直角三角形,利用勾股定理建立关系式.
 x2+x
x2+x分析:连接O1C,O1O,如图所示,由圆O1与AB相切,根据切线的性质得到O1C⊥AB,O1C为半径y,再由半圆直径AB的长,求出半径OA的长,用OA-AC及AC=x,表示出OC的长,由两圆内切,得到圆心距等于两半径之差,由大圆的半径2与小圆半径y之差表示出O1O,在直角三角形O1CO中,利用勾股定理列出关系式,将各自的值代入,化简后即可得到y与x的关系式.
解答:连接O1C,O1O,如图所示:

∵圆O1与AB相切与点C,且圆O1的半径为y,
∴O1C⊥AB,O1C=y,
∵AB=4,
∴OA=2,又AC=x,
∴OC=OA-AC=2-x,
∵圆O1与圆O内切,
∴圆心距d=OO1=2-y,
在Rt△O1CO中,根据勾股定理得:O1C2+CO2=O1O2,
即y2+(2-x)2=(2-y)2,
化简得:y=-
 x2+x.
x2+x.故答案为:y=-
 x2+x
x2+x点评:此题考查了两圆相切的性质,切线的性质,以及勾股定理,利用了数形结合的思想,当两圆外切时,圆心角等于两半径之和;当两圆内切时,圆心距等于两半径之差,解本题的关键是连接圆心与切点,构造直角三角形,利用勾股定理建立关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
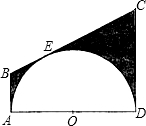 如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.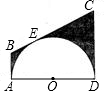 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
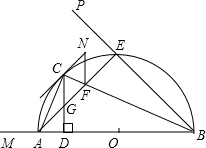 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( ) 如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.