��Ŀ����
����Ŀ��ͼ����һ����Ϊ![]() ����Ϊ
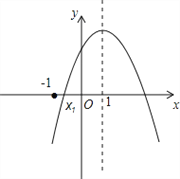
����Ϊ![]() �ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ��ͼ�ڵ���״ƴ��һ�������Σ�
�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ��ͼ�ڵ���״ƴ��һ�������Σ�




��1��ͼ���е���Ӱ���ֵ����Ϊ______��
��2���۲�ͼ������д����������ʽ![]() ��
��![]() ��
��![]() ֮��ĵ�����ϵ�ǣ�__________��
֮��ĵ�����ϵ�ǣ�__________��
��3��ʵ����������������ʽ������ͼ�ε��������ʾ����ͼ�ۣ�����ʾ��___________��
��4��������ͼ���ṩ�����ɿ鳤���κ�������ӲֽƬͼ�Σ���ƴ�����εķ����������ж�������ʽ������ʽ�ֽ⣺![]() ��Ҫ����ͼ�ܵĿ��л���ͼ�Σ�д���ֽ����ʽ��
��Ҫ����ͼ�ܵĿ��л���ͼ�Σ�д���ֽ����ʽ��
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��ͼ�μ�������
����4��ͼ�μ�������![]() ��
��
��������
��1���ô������ε������ȥ4��С�����ε�������������Ӱ���ֵ������
��2�����ô������ε��������4��С�����ε��������Ӱ�������֮�ɵó��𰸣�
��3�����ô��ε��������3��С�����κ�3��С�����ε����֮�ͼ��ɵó��𰸣�
��4���������ɸ�С�����κ�������ƴ��һ�����Σ�ʹ���ǵ����֮��Ϊ![]() ��Ȼ�����ƴ�ɵĴ��ε������ʽ���ɵõ���ʽ�ֽ�Ľ����
��Ȼ�����ƴ�ɵĴ��ε������ʽ���ɵõ���ʽ�ֽ�Ľ����
��1����Ӱ���ֵ����Ϊ
![]() ��
��
��2�����ݣ�1���Ľ����֪��![]() ��
��
��3�����ε�����ɱ�ʾΪ![]() ��
��
���ε����Ҳ�ɱ�ʾΪ![]() ��
��
��![]() ��
��
��4�������ɸ�С�����κ������ε����֮��Ϊ![]() ��
��
��ƴ�ɵĴ����л����1���߳�Ϊm�������Σ�3���߳�Ϊn�������κ�4����Ϊm����Ϊn�ij����Σ�
ƴ�ɵĴ�����ͼ��
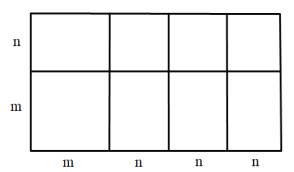
���ε�����ɱ�ʾΪ![]()
��![]() ��
��

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�����Ŀ��ijУ���꼶1������ίԱͳ����ȫ��ͬѧ60�������Ĵ����������Ƴ�����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
���� | 80��x��100 | 100��x��120 | 120��x��140 | 140��x��160 | 160��x��180 | 180��x��200 |
Ƶ�� | a | 4 | 12 | 16 | 8 | 3 |
���ͼ������������⣺
��1��a=�� ����
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��д��ȫ���������� �����������������120��x��140����Ƶ�ʣ���ȷ��0.01��
��4������������������140��ѧ���ɼ�Ϊ���㣬������ѧ������ռȫ���������İٷ�֮����