题目内容
利用图形，我们可以求出tan30°的值．如图，在Rt△ABC中，已知∠C=90°，AB=2，AC=1，可求出∠B=30°，tan30°=| AC |
| BC |
| 1 | ||
|
| ||
| 3 |
分析：根据角平分线的性质以及勾股定理首先求出CD的长，进而得出tan15°=
求出即可．
| CD |
| BC |
解答：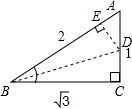
解：作∠B的平分线交AC于点D，作DE⊥AB，垂足为E，
∵BD平分∠ABC，CD⊥BC，DE⊥AB，
∴CD=DE，
设CD=x，则AD=1-x，AE=2-BC=2-BE=2-
在Rt△ADE中，
CD2+AE2=AD2
x2+（2-
）2=（1-x）2，
解得：x=2
-3，
∴tan15°=
=
=2-
．
解：作∠B的平分线交AC于点D，作DE⊥AB，垂足为E，∵BD平分∠ABC，CD⊥BC，DE⊥AB，
∴CD=DE，
设CD=x，则AD=1-x，AE=2-BC=2-BE=2-
| 3 |
在Rt△ADE中，
CD2+AE2=AD2
x2+（2-
| 3 |
解得：x=2
| 3 |
∴tan15°=
| CD |
| BC |
2
| ||
|
| 3 |
点评：此题主要考查了解直角三角形和勾股定理等知识，根据已知得出CD的长是解题关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
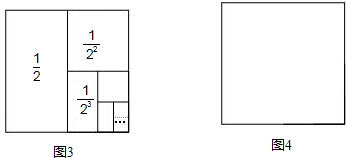
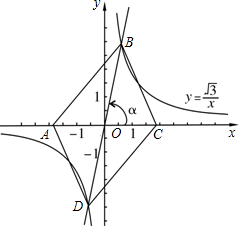我们容易发现：反比例函数的图象是一个中心对称图形．你可以利用这一结论解决问题．如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x轴所在的直线绕着原点O逆时针旋转α度角后的图形．若它与反比例函数
式子
