Question

如图7，在△ABC中，AB=AC，以AB为直径的⊙O交AC于点E，交BC于点D，连结BE、AD交于点P. 求证：

（1）D是BC的中点；

（2）△BEC ∽△ADC；

（3）AB× CE=2DP×AD．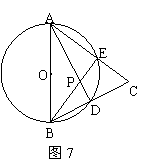

Answer 1

证明：（1）∵AB是直径   ∴∠ADB= 90°即AD⊥BC   （1分）

        又∵AB=AC     ∴D是BC的中点           （3分）

     （2）在△BEC与 △ADC中，

          ∵∠C=∠C     ∠CAD=∠CBE             （5分）

          ∴△BEC ∽△ADC                       （6分）

     （3）∵△BEC ∽△ADC    ∴ 

          又∵D是BC的中点   ∴2BD=2CD=BC

         ∴    则    ①   （7分）

         在△BPD与 △ABD中， 

          有  ∠BDP=∠BDA    

又∵AB=AC      AD⊥BC

∴∠CAD=∠BAD     

          又∵∠CAD=∠CBE     ∴∠DBP=∠DAB

          ∴△BPD ∽△ABD                          （8分）

          ∴   则   ②     （9分）

          ∴由①，②得：

          ∴                     （10分）