题目内容
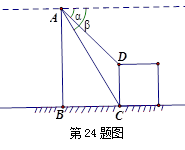
如图，直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α为45°，底端C点的俯角β为60°，此时直升飞机与建筑物CD的水平距离BC为60米，求建筑物CD的高．（结果保留根号）分析：首先过点D作DE⊥AB于E，得出AE=DE•tan45°，进而求出AB=BC•tan60°即可求出CD．
解答：
解：过点D作DE⊥AB于E，依据题意，
在Rt△ADE中，∠ADE=∠α=45°
∴AE=DE•tan45°=BC•tan45°=60，
在Rt△ACB中，∵∠ACB=∠β=60°，
∴AB=BC•tan60°=60
，
∴CD=BE=AB=AE=（60
-60）米．
答：建筑物CD的高为（60
-60）米．
解：过点D作DE⊥AB于E，依据题意，在Rt△ADE中，∠ADE=∠α=45°
∴AE=DE•tan45°=BC•tan45°=60，
在Rt△ACB中，∵∠ACB=∠β=60°，
∴AB=BC•tan60°=60
| 3 |
∴CD=BE=AB=AE=（60
| 3 |
答：建筑物CD的高为（60
| 3 |
点评：此题主要考查了仰角与俯角的应用，根据已知构造直角三角形利用锐角三角函数关系得出是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
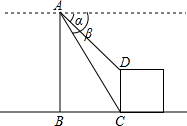
关于三角函数有如下的公式：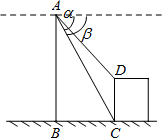
如图，直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α为45°，底端C点的俯角β为60°，此时飞机与建筑物CD的水平距离BC为42米，求建筑物CD的高．
