题目内容
已知⊙O的半径为5cm,AB是弦,P是直线AB上的一点,PA=3cm,AB=8cm,则tan∠OPB的值为________.
3或
分析:点P是直线AB上的一点,则P可能在线段BE上,或BE的延长线上,因分两种情况进行讨论,过O作AB的垂线,根据三角函数的定义就可以求解即可求得答案.
解答: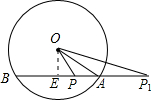 解:作OE⊥AB,则EA=8×
解:作OE⊥AB,则EA=8× =4cm.
=4cm.
∵PA=3cm,
∴EP=4-3=1cm.
又⊙O的半径为5,∴OE= =3cm.
=3cm.
当P在线段BE上时:tan∠OPB= =3;
=3;
当P在线段EB的延长线上时:设P是P1,则tan∠OP1B=3÷(1+3+3)= .
.
故答案为:3或 .
.
点评:根据勾股定理和垂径定理求出直角三角形各边长,再根据三角函数的定义解答.此题难度适中,解题的关键是注意数形结合思想与分类讨论思想的应用.

分析:点P是直线AB上的一点,则P可能在线段BE上,或BE的延长线上,因分两种情况进行讨论,过O作AB的垂线,根据三角函数的定义就可以求解即可求得答案.
解答:
 解:作OE⊥AB,则EA=8×
解:作OE⊥AB,则EA=8× =4cm.
=4cm.∵PA=3cm,
∴EP=4-3=1cm.
又⊙O的半径为5,∴OE=
 =3cm.
=3cm.当P在线段BE上时:tan∠OPB=
 =3;
=3;当P在线段EB的延长线上时:设P是P1,则tan∠OP1B=3÷(1+3+3)=
 .
.故答案为:3或
 .
.点评:根据勾股定理和垂径定理求出直角三角形各边长,再根据三角函数的定义解答.此题难度适中,解题的关键是注意数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
 如图,已知⊙O的半径为5,弦AB=6,M是AB上任意一点,则线段OM的长可能是( )
如图,已知⊙O的半径为5,弦AB=6,M是AB上任意一点,则线段OM的长可能是( )| A、2.5 | B、3.5 | C、4.5 | D、5.5 |
 如图,已知⊙O的半径为5,弦AB=8,M是AB上任意一点,则线段OM的长可以是( )
如图,已知⊙O的半径为5,弦AB=8,M是AB上任意一点,则线段OM的长可以是( )| A、1.5 | B、2.5 | C、4.5 | D、5.5 |