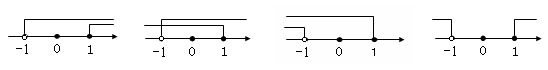题目内容
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.


解:(1)证明:∵AB=AC,∴∠ABC=∠C,
∵∠C=∠D,∴∠ABC=∠D,
又∵∠BAE=∠EAB,∴△ABE∽△ADB, …………………………………3分
(2)∵△ABE∽△ADB,∴ ,∴
,∴
∴AB= . …………………………………6分
. …………………………………6分
(3)直线FA与⊙O相切,理由如下:
连接OA,∵BD为⊙O的直径,∴∠BAD=90°,
∴ ,
,
BF=BO= ,
,
∵AB= ,∴
,∴
∴直线FA与⊙O相切 . …………………………………10分

练习册系列答案
相关题目
 D.
D.
 分解因式的结果是 .
分解因式的结果是 . 
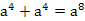 . B.
. B. 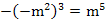
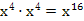 D.
D. 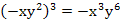
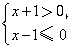 的解集表示在数轴上,正确的为图中的( )
的解集表示在数轴上,正确的为图中的( )