题目内容
已知PA,PB切⊙O于点A,B,∠APB=40°.点C在⊙O上(点C异于A,B点),则∠ACB= .
考点:切线的性质
专题:
分析:①连接AB.根据切线长定理和弦切角定理求解.
②由于已知中已知角∠APB=40°,且PA、PB是圆O的切线,A、B分别为切点,我们可以连接OA、OB,借助∠AOB为中间角,探寻中间角与已知角和未知角的关系,从而求解.
②由于已知中已知角∠APB=40°,且PA、PB是圆O的切线,A、B分别为切点,我们可以连接OA、OB,借助∠AOB为中间角,探寻中间角与已知角和未知角的关系,从而求解.
解答: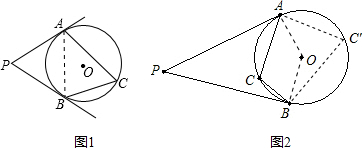 解:①如图1,连接AB,由切线长定理知AP=BP,
解:①如图1,连接AB,由切线长定理知AP=BP,
则∠PAB=∠PBA=(180°-∠APB)÷2=(180°-∠40)÷2=70°,
由弦切角定理知,∠C=∠PAB=70°,
若C点在劣弧AB上,则根据圆内接四边形的性质知,∠C=180°-70°=110°;
②如图2,解:连接OA、OB,在优弧AB取点C′,连接AC′,BC′,
∵OA⊥PA,OB⊥PB,
∴∠APB=180°-∠AOB,
∵∠APB=40°,
∴∠AOB=180°-40°=140°,
∴∠AC′B=
×140°=70°,
∵∠ACB+∠AC′B=180°,
∴∠ACB=110°.
综上所述,∠ACB=110°.
故答案是:110°.
 解:①如图1,连接AB,由切线长定理知AP=BP,
解:①如图1,连接AB,由切线长定理知AP=BP,则∠PAB=∠PBA=(180°-∠APB)÷2=(180°-∠40)÷2=70°,
由弦切角定理知,∠C=∠PAB=70°,
若C点在劣弧AB上,则根据圆内接四边形的性质知,∠C=180°-70°=110°;
②如图2,解:连接OA、OB,在优弧AB取点C′,连接AC′,BC′,
∵OA⊥PA,OB⊥PB,
∴∠APB=180°-∠AOB,
∵∠APB=40°,
∴∠AOB=180°-40°=140°,
∴∠AC′B=
| 1 |
| 2 |
∵∠ACB+∠AC′B=180°,
∴∠ACB=110°.
综上所述,∠ACB=110°.
故答案是:110°.
点评:本题考查的是切线的性质定理,四边形的对角互补以及圆周角是对应圆心角的一半的性质,解题时,要注意对点C的不同位置进行分类讨论.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 物理学定律告诉我们:光线经平面镜反射,光线与平面镜所成的角等于反射线与平面镜所成的角.现在有一束光线与水平面成60°的角照射地面,为使这束光线经过平面镜反射后成水平光线,如图所示在地面AB上放置一个平面镜CD,则平面镜CD与地面AB所成的∠DCB应为( )
物理学定律告诉我们:光线经平面镜反射,光线与平面镜所成的角等于反射线与平面镜所成的角.现在有一束光线与水平面成60°的角照射地面,为使这束光线经过平面镜反射后成水平光线,如图所示在地面AB上放置一个平面镜CD,则平面镜CD与地面AB所成的∠DCB应为( )