题目内容
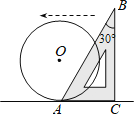
【题目】如图，半径为4的
与含有
角的真角三角板ABC的边AC切于点A，将直角三角板沿CA边所在的直线向左平移，当平移到AB与相切时，该直角三角板平移的距离为
A. 2 B. 
C. 4 D. 
【答案】D
【解析】
根据题意画出平移后的图形，如图所示，设平移后的
与圆O相切于点D，连接OD，OA，AD，过O作
，根据垂径定理得到E为AD的中点，由平移前AC与圆O相切，切点为A点，根据切线的性质得到OA与AC垂直，可得
为直角，由
与
为圆O的两条切线，根据切线长定理得到
，再根据
，根据有一个角为
的等腰三角形为等边三角形可得出三角形
为等边三角形，平移的距离
，且
，由
求出
为
，在直角三角形AOE中，由锐角三角函数定义求出AE的长，由
可求出AD的长，即为平移的距离．
解：根据题意画出平移后的图形，如图所示：
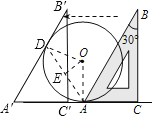
设平移后的与圆O相切于点D，连接OD，OA，AD，
过O作，可得E为AD的中点，
平移前圆O与AC相切于A点，
，即
，
平移前圆O与AC相切于A点，平移后圆O与
相切于D点，
即与为圆O的两条切线，
，又，
为等边三角形，
，
，
，
在
中，
，
，
，
，
，
则该直角三角板平移的距离为
．
故选：D．
练习册系列答案
相关题目
