题目内容
矩形纸片ABCD中,AB=5,AD=4.
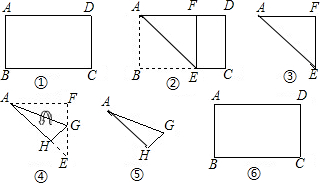
(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;
(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).
 | |||||
 | |||||
| |||||
解:(1)正方形的最大面积是16.
设AM=x(0≤x≤4) ,
则MD=4-x.
∵四边形MNEF是正方形,
∴MN=MF,∠AMN+∠FMD=90°.
 ∵∠AMN+∠ANM=90°,
∵∠AMN+∠ANM=90°,
∴∠ANM=∠FMD.
∴Rt△ANM≌Rt△DMF.
∴DM=AN.
∴![]()
![]()
∵函数![]() 的开口向上,
的开口向上,
对称轴是x=2,
函数图象如图所示,
∵0≤x≤4,
∴当x=0或x=4时,
正方形MNEF的面积最大.
最大值是16.……………………5′
(2)如图,画出分割线7′;拼出图形9′.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
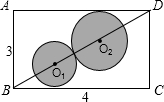 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )
如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )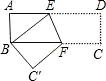 如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为
如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为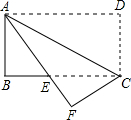 如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.
如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.