题目内容
如图(1),Rt ∆ABC中,![]() 垂足为D.AF平分∠CAB.交CD于点E,交CB于点F.
垂足为D.AF平分∠CAB.交CD于点E,交CB于点F.
1.求证:CE=CF;
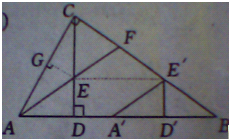
2.将图(1)中的∆ADE沿AB向右平移到∆A'D'E'的位置,使点E’落在BC边上,其它条件不变,如图(2)所示.试猜想:BE’与CF有怎样的数量关系?请证明你的结论.
1.证明:因为AF平分∠CAB,
所以∠CAF= ∠EAD, (1分)
因为:∠ACB=900
所以:∠CAF+∠CFA=900 (2分)
因为:CD⊥AB于D
所以:∠EAD+∠AED=900
所以:∠CFA=∠AED,又∠AED=∠CEF,
所以:∠CFA=∠CEF,
所以;CE=CF
2.猜想:BE’=CF (5分)
证明:如图,过点E作EG⊥AC于点G
又AF平分∠CAB,ED⊥AB、ED⊥AB,EG⊥AC
所以:ED=EG,
由平移的性质可知:D’E’=DE,
所以:D’E’=GE
因为:∠ACB=900
所以:∠ACD+∠DCB=900
因为:CD⊥AB于点D
所以:∠B+∠DCB=900
所以:∠ACD=∠B
在Rt∆CEG与Rt∆BE’D’中
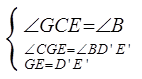
所以:∆CEG≅∆BE’D’ (8分)
所以:CE=BE’
由(1)可知CE=CF。
所以:BE’=CF (9分)
解析:(1)根据平分线的定义可知∠CAF=∠EAD,再根据已知条件以及等量代换即可证明CE=CF,
(2)根据题意作辅助线过点E作EG⊥AC于G,根据平移的性质得出D′E′=DE,再根据已知条件判断出△CEG≌△BE′D′,可知CE=BE′,再根据等量代换可知BE′=CF.

 27、如图,已知RT△ABC与RT△DEF不相似,其中∠C、∠F为直角,能否分别将这两个三角形各分割成两个三角形,使△ABC所分的每个三角形与△DEF所分成的每个三角形分别对应相似?若能,请设计出一种分割方案.
27、如图,已知RT△ABC与RT△DEF不相似,其中∠C、∠F为直角,能否分别将这两个三角形各分割成两个三角形,使△ABC所分的每个三角形与△DEF所分成的每个三角形分别对应相似?若能,请设计出一种分割方案. 3、将如图所示的Rt△ABC绕直角边AC旋转一周,所得几何体的主视图是( )
3、将如图所示的Rt△ABC绕直角边AC旋转一周,所得几何体的主视图是( ) 如图,分别以Rt△XYZ的直角边和斜边为边向形外作正方形AXZF、BCYX、DEZY,若直角边YZ=1,XZ=2,则六边形ABCDEF的面积为
如图,分别以Rt△XYZ的直角边和斜边为边向形外作正方形AXZF、BCYX、DEZY,若直角边YZ=1,XZ=2,则六边形ABCDEF的面积为 如图,将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下,已知楔子斜面的倾斜角为20°,要使木桩向上移动5cm,则楔子沿水平方向前进(如箭头所示)了
如图,将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下,已知楔子斜面的倾斜角为20°,要使木桩向上移动5cm,则楔子沿水平方向前进(如箭头所示)了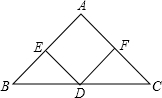 如图,已知Rt△ABC中,AB=AC,D是斜边BC的中点,将直角三角尺的直角顶点置于点D,两直角边分别与AB,AC交于点E,F.求证:DE=DF.
如图,已知Rt△ABC中,AB=AC,D是斜边BC的中点,将直角三角尺的直角顶点置于点D,两直角边分别与AB,AC交于点E,F.求证:DE=DF.