题目内容
问题提出:
平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
(1)当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);
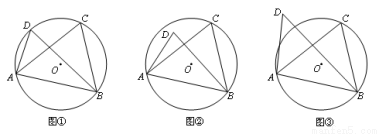
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.
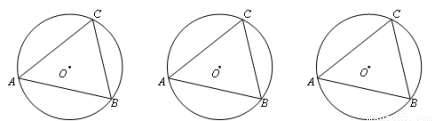
此时有 , 此时有 , 此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
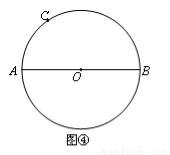
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA,CB;
②在上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
练习册系列答案
相关题目
某科研机构对我区400户有两个孩子的家庭进行了调查,得到了表格中的数据,其中(男,女)代表第一个孩子是男孩,第二个孩子是女孩,其余类推.由数据,请估计我区两个孩子家庭中男孩与女孩的人数比为 : .
类别 | 数量(户) |
(男,男) | 101 |
(男,女) | 99 |
(女,男) | 116 |
(女,女) | 84 |
合计 | 400 |


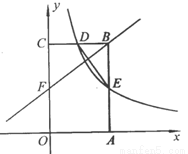
 的顶点
的顶点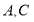 分别在
分别在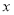 轴和
轴和 轴上,点
轴上,点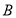 的坐标为
的坐标为 .双曲线
.双曲线 的图像经过
的图像经过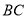 的中点
的中点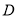 ,且与
,且与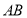 交于点
交于点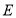 ,连接
,连接 .
.
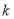 的值及点
的值及点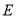 的坐标;
的坐标;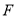 是边上一点,且ΔFCB∽ΔDBE,求直线
是边上一点,且ΔFCB∽ΔDBE,求直线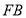 的解析式
的解析式 的解集是( )
的解集是( ) 上,分别经过A,B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2=( )。
上,分别经过A,B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2=( )。


 =2,
=2, =4,则甲的射击成绩更稳定
=4,则甲的射击成绩更稳定