Question

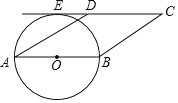
【题目】如图，在平行四边形ABCD中，AD=4，∠C=30°，⊙O与AD相交于点F，AB为⊙O的直径，⊙O与CD的延长线相切于点E，则劣弧FE的长为_________

Answer 1

【答案】

【解析】

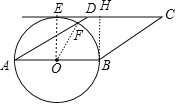
连接OE、OF，作BH⊥CD于H，如图，利用切线的性质得OE⊥CD，再利用平行四边形的性质得CD∥AB，∠A=∠C=30°，BC=AD=4，从而得到四边形OEHB为矩形，则BH=OE，计算出BH=2，然后求出∠EOF的度数后利用弧长公式求解．

连接OE、OF，作BH⊥CD于H，如图，

∵CD为切线，

∴OE⊥CD，

∵四边形ABCD为平行四边形，

∴CD∥AB，∠A=∠C=30°，BC=AD=4，

∴OE⊥AB，

易得四边形OEHB为矩形，

∴BH=OE，

在Rt△BCH中，BH=BC=2，

∵OA=OC，

∴∠A=∠OCA=30°，

∴∠BOF=∠A+∠OFA=60°，

∴∠EOF=30°，

∴劣弧FE的长=．

故答案为：．