题目内容
 已知:如图1,∠AOB=70°.
已知:如图1,∠AOB=70°.(1)如图2,射线OC在∠AOB的内部,OD平分∠AOC,若∠BOD=40°,求∠BOC的度数;
(2)若∠BOD=3∠B0C(∠BOC<45°),且∠AOD=
| 1 | 2 |
分析:(1)根据角平分线的性质得出∠AOC=2∠AOD=60°,进而得出∠BOC=∠AOB-∠AOC即可;
(2)①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:i)若射线OD在∠AOC内部,ii)若射线OD在∠AOB外部,
②当射线OD在∠AOB外部时,i)若射线DO在∠AOB内部,ii)若射线OD在∠AOB外部分别求出即可.
(2)①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:i)若射线OD在∠AOC内部,ii)若射线OD在∠AOB外部,
②当射线OD在∠AOB外部时,i)若射线DO在∠AOB内部,ii)若射线OD在∠AOB外部分别求出即可.
解答: 解:(1)∵∠AOB=70°,∠BOD=40°,
解:(1)∵∠AOB=70°,∠BOD=40°,
∴∠AOD=∠AOB-∠BOD=70°-40°=30°,
∵OD是∠AOC的平分线,
∴∠AOC=2∠AOD=60°,
∴∠BOC=∠AOB-∠AOC=10°;
(2)设∠BOC=α,
∴∠BOD=3∠BOC=3α,
依据题意,分两种情况:
①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:
i)若射线OD在∠AOC内部,如图2,
∴∠COD=∠BOD-∠BOC=2α,
∵∠AOD=
∠AOC,
∴∠AOD=∠COD=2α,
∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,
∴α=14°,
∴∠BOC=14°;
ii)若射线OD在∠AOB外部,如图3,
∴ ∠COD=∠BOD-∠BOC=2α,
∠COD=∠BOD-∠BOC=2α,
∵∠AOD=
∠AOC,
∴∠AOD=
∠COD=
α,
∴∠AOB=∠BOD-∠AOD=3α-
α=
α=70°,
∴α=30°,
∴∠BOC=30°;
②当射线OD在∠AOB外部时,
依据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD=
∠AOC,
∴射线OD的位置也只有两种可能:
i)若射线DO在∠AOB内部,如图4,
则∠COD=∠BOC+∠BOD=4α,
∵∠AOD=
∠AOC,
∴∠AOD=∠COD=4α,
∴∠AOB=∠BOD+∠AOD=4α,
∴AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
∴∠BOC=10°
ii)若射线OD在∠AOB外部,如图5,
则∠COD=∠BOC+∠DOB=4α,
∵∠AOD=
∠AOC,
∴∠AOD=
∠COD=
α,
∴∠AOB=∠BOD-∠AOD=3α-
α=
α=70°,
∴α=42°,
∴∠BOC=42°,
综上所述:∠BOC的度数分别是10°,14°,30°,42°.
 解:(1)∵∠AOB=70°,∠BOD=40°,
解:(1)∵∠AOB=70°,∠BOD=40°,∴∠AOD=∠AOB-∠BOD=70°-40°=30°,
∵OD是∠AOC的平分线,
∴∠AOC=2∠AOD=60°,
∴∠BOC=∠AOB-∠AOC=10°;
(2)设∠BOC=α,
∴∠BOD=3∠BOC=3α,
依据题意,分两种情况:
①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:
i)若射线OD在∠AOC内部,如图2,
∴∠COD=∠BOD-∠BOC=2α,
∵∠AOD=
| 1 |
| 2 |
∴∠AOD=∠COD=2α,
∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,
∴α=14°,
∴∠BOC=14°;
ii)若射线OD在∠AOB外部,如图3,
∴
 ∠COD=∠BOD-∠BOC=2α,
∠COD=∠BOD-∠BOC=2α,∵∠AOD=
| 1 |
| 2 |
∴∠AOD=
| 1 |
| 3 |
| 2 |
| 3 |
∴∠AOB=∠BOD-∠AOD=3α-
| 2 |
| 3 |
| 7 |
| 3 |
∴α=30°,
∴∠BOC=30°;
②当射线OD在∠AOB外部时,
依据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD=
| 1 |
| 2 |

∴射线OD的位置也只有两种可能:
i)若射线DO在∠AOB内部,如图4,
则∠COD=∠BOC+∠BOD=4α,
∵∠AOD=
| 1 |
| 2 |
∴∠AOD=∠COD=4α,
∴∠AOB=∠BOD+∠AOD=4α,
∴AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,

∴∠BOC=10°
ii)若射线OD在∠AOB外部,如图5,
则∠COD=∠BOC+∠DOB=4α,
∵∠AOD=
| 1 |
| 2 |
∴∠AOD=
| 1 |
| 3 |
| 4 |
| 3 |
∴∠AOB=∠BOD-∠AOD=3α-
| 4 |
| 3 |
| 5 |
| 3 |
∴α=42°,
∴∠BOC=42°,
综上所述:∠BOC的度数分别是10°,14°,30°,42°.
点评:此题主要考查了角平分线的性质以及分类讨论思想的应用,根据已知正确分射线OD在∠AOB外部或内部得出是解题关键.

练习册系列答案
相关题目
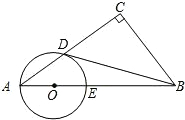 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A. 21、已知:如图,在△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
21、已知:如图,在△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.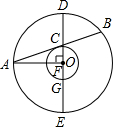 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB和小圆相切于点C,过点C作大圆的弦DE,使DE⊥OA,垂足为F,DE交小圆于另一点G.求证:AF•AO=DC•DG.
已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB和小圆相切于点C,过点C作大圆的弦DE,使DE⊥OA,垂足为F,DE交小圆于另一点G.求证:AF•AO=DC•DG. (2012•广州模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
(2012•广州模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点. (2013•安溪县质检)已知:如图,BC=EF,∠1=∠2,AO=DO.求证:AB=DE.
(2013•安溪县质检)已知:如图,BC=EF,∠1=∠2,AO=DO.求证:AB=DE.