题目内容
 已知点A为一次函数y=-x的图象与反比例函数y=-
已知点A为一次函数y=-x的图象与反比例函数y=- 的图象在第二象限内的交点,点B在x轴的正半轴上,且OA=
的图象在第二象限内的交点,点B在x轴的正半轴上,且OA= OB,那么△AOB的面积为
OB,那么△AOB的面积为
- A.4

- B.4
- C.2

- D.16
A
分析:欲求OAB的面积,已知点A是一次函数y=-x的图象与反比例函数y=- 的图象在第二象限内的交点,可求出点A的坐标,从而得到△AOB的高,结合已知OA=
的图象在第二象限内的交点,可求出点A的坐标,从而得到△AOB的高,结合已知OA= OB,求得底边OB,从而求出面积.
OB,求得底边OB,从而求出面积.
解答:依题意A点的坐标满足方程组
∴
∴A(-2,-2)
∴OA=2
∵OB=2OA=4
∴S△AOB= OB×2=
OB×2= ×4
×4 ×2=4
×2=4 .
.
故选A.
点评:此题主要考查反比例函数的性质,注意通过解方程组求出交点坐标.同时要注意运用数形结合的思想.
分析:欲求OAB的面积,已知点A是一次函数y=-x的图象与反比例函数y=-
 的图象在第二象限内的交点,可求出点A的坐标,从而得到△AOB的高,结合已知OA=
的图象在第二象限内的交点,可求出点A的坐标,从而得到△AOB的高,结合已知OA= OB,求得底边OB,从而求出面积.
OB,求得底边OB,从而求出面积.解答:依题意A点的坐标满足方程组

∴

∴A(-2,-2)
∴OA=2

∵OB=2OA=4

∴S△AOB=
 OB×2=
OB×2= ×4
×4 ×2=4
×2=4 .
.故选A.
点评:此题主要考查反比例函数的性质,注意通过解方程组求出交点坐标.同时要注意运用数形结合的思想.

练习册系列答案
相关题目
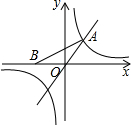 (北师大版)如图,已知点A是一次函数y=x的图象与反比例函数y=
(北师大版)如图,已知点A是一次函数y=x的图象与反比例函数y= 已知点A为一次函数y=-x的图象与反比例函数y=-
已知点A为一次函数y=-x的图象与反比例函数y=-