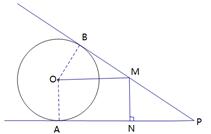
题目内容
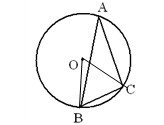
如图,已知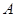 ,
,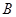 两点的坐标分别为(
两点的坐标分别为(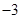 ,
, ),(
),( ,
,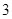 ),⊙
),⊙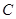 的圆心坐标为(
的圆心坐标为(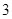 ,
, ),并与
),并与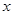 轴交于坐标原点
轴交于坐标原点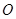 .若
.若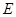 是⊙
是⊙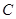 上的一个动点,线段
上的一个动点,线段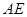 与
与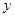 轴交于点
轴交于点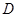 .
.
(1)线段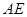 长度的最小值是_________,最大值是_________;
长度的最小值是_________,最大值是_________;
(2)当点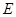 运动到点
运动到点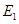 和点
和点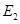 时,线段
时,线段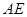 所在的直线与⊙
所在的直线与⊙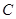 相切,求由
相切,求由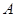
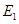 、
、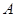
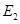 、弧
、弧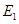
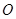
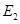 所围成的图形的面积;
所围成的图形的面积;
(3)求出△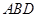 的最大值和最小值
的最大值和最小值
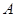 ,
,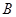 两点的坐标分别为(
两点的坐标分别为(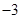 ,
, ),(
),( ,
,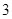 ),⊙
),⊙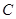 的圆心坐标为(
的圆心坐标为(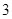 ,
, ),并与
),并与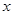 轴交于坐标原点
轴交于坐标原点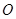 .若
.若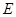 是⊙
是⊙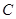 上的一个动点,线段
上的一个动点,线段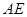 与
与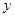 轴交于点
轴交于点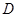 .
.
(1)线段
 长度的最小值是_________,最大值是_________;
长度的最小值是_________,最大值是_________;(2)当点
 运动到点
运动到点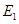 和点
和点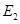 时,线段
时,线段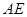 所在的直线与⊙
所在的直线与⊙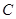 相切,求由
相切,求由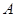
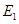 、
、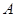
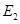 、弧
、弧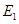
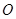
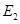 所围成的图形的面积;
所围成的图形的面积;(3)求出△
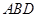 的最大值和最小值
的最大值和最小值(1)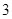 ,
, (2)
(2)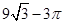 (3)最大值为
(3)最大值为 ,最小值为
,最小值为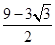
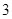 ,
, (2)
(2)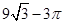 (3)最大值为
(3)最大值为 ,最小值为
,最小值为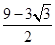
(1)由图得线段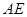 长度的最小值是3,最大值是9
长度的最小值是3,最大值是9
(2)根据三角形AE1C的面积减去扇形COE1的面积乘以2求得
(3)由于AB的长为定值,若△ABD的面积最大,则BD的长最长,此时AE与⊙相切且位于x轴的下方;可连接CE,在Rt△ADC中,由勾股定理求得AE的长,即可得到△AEC的面积;易证得△ADO∽△ACE,可以求出OD的长,进而可得出△AOB和△AOE的面积和,由此求出△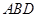 的最大值.同理,求得△
的最大值.同理,求得△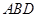 的最小值
的最小值
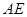 长度的最小值是3,最大值是9
长度的最小值是3,最大值是9(2)根据三角形AE1C的面积减去扇形COE1的面积乘以2求得
(3)由于AB的长为定值,若△ABD的面积最大,则BD的长最长,此时AE与⊙相切且位于x轴的下方;可连接CE,在Rt△ADC中,由勾股定理求得AE的长,即可得到△AEC的面积;易证得△ADO∽△ACE,可以求出OD的长,进而可得出△AOB和△AOE的面积和,由此求出△
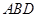 的最大值.同理,求得△
的最大值.同理,求得△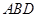 的最小值
的最小值
练习册系列答案
相关题目
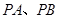 分别与
分别与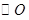 相切于点
相切于点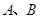 ,点
,点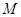 在
在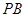 上,且
上,且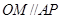 ,
,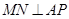 ,垂足为
,垂足为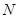 .
.
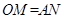 ;
;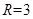 ,
,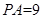 ,求
,求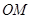 的长
的长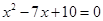 的两个根,O1O2
的两个根,O1O2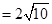 ,则⊙O1和⊙O2的位置关
,则⊙O1和⊙O2的位置关
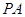 是
是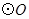 的切线,切点为A,PA=2
的切线,切点为A,PA=2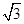 ,∠APO=30°,则
,∠APO=30°,则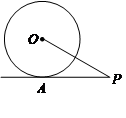
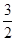 B.2 C.1 D.
B.2 C.1 D.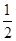

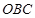 ,
,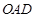 的半径之间的关系是
的半径之间的关系是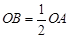 ,则弧BC的长是弧AD长的( )
,则弧BC的长是弧AD长的( )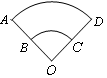
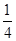 倍
倍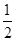 倍
倍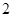 倍
倍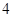 倍
倍