题目内容
（2012•松江区一模）已知在△ABC中，AB=AC=5cm，BC=5
，那么∠A=
| 3 |
120
120
度．分析：根据等腰三角形三线合一的性质，作AD⊥BC，可得BD=DC，运用特殊角的三角函数值可求∠BAC的度数，即可求解．
解答：解：
作AD⊥BC于D，
∵AB=AC=5cm，底边BC=5
cm，
∴AD是∠A的平分线，BD=DC=
BC=
，
∴Sin∠BAD=
=
，
∴∠BAD=60°，
∴∠BAC=120°．
故答案为：120．
作AD⊥BC于D，∵AB=AC=5cm，底边BC=5
| 3 |
∴AD是∠A的平分线，BD=DC=
| 1 |
| 2 |
5
| ||
| 2 |
∴Sin∠BAD=
| BD |
| AB |
| ||
| 2 |
∴∠BAD=60°，
∴∠BAC=120°．
故答案为：120．
点评：此题主要考查等腰三角形的性质和特殊角的三角函数值的理解和掌握，难度不大，属于基础题．
练习册系列答案
ABC考王全优卷系列答案
相关题目
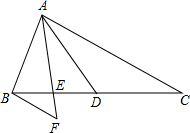（2012•松江区一模）已知：如图，在△ABC中，AD是边BC上的中线，点E在线段BD上，且BE=ED，过点B作BF∥AC，交线段AE的延长线于点F．