题目内容
 如图,⊙O阴影部分为残缺部分,现要在剩下部分裁去一个最大的正方形,若OP=2,⊙O半径为5,则裁去的最大正方形边长为多少?
如图,⊙O阴影部分为残缺部分,现要在剩下部分裁去一个最大的正方形,若OP=2,⊙O半径为5,则裁去的最大正方形边长为多少?
- A.7
- B.6
- C.5
- D.4
B
分析:如图,正方形ABCD是最大的正方形,OP⊥AB,根据垂径定理,可得PF垂直平分CD,可设正方形ABCD的边长为x,在直角△OFD中,根据勾股定理,可求出x,即正方形的边长.
解答: 解:如图:正方形ABCD是最大的正方形,OP⊥AB,
解:如图:正方形ABCD是最大的正方形,OP⊥AB,
延长PO交CD于点F,
∴OF⊥CD,DF=CF,AD=PF,
∵OP=2,⊙O半径为5,
可设正方形ABCD的边长为x,
则DF= ,OF=x-2,
,OF=x-2,
∴在直角△OFD中,(x-2)2+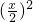 =52,
=52,
解得x=6;
即正方形ABCD的边长为6.
故选B.
点评:本题主要考查了垂径定理及勾股定理的应用,本题结合已知构建直角△OFD,是解答的关键,解决问题时,要善于把问题与数学中的理论知识联系起来.
分析:如图,正方形ABCD是最大的正方形,OP⊥AB,根据垂径定理,可得PF垂直平分CD,可设正方形ABCD的边长为x,在直角△OFD中,根据勾股定理,可求出x,即正方形的边长.
解答:
 解:如图:正方形ABCD是最大的正方形,OP⊥AB,
解:如图:正方形ABCD是最大的正方形,OP⊥AB,延长PO交CD于点F,
∴OF⊥CD,DF=CF,AD=PF,
∵OP=2,⊙O半径为5,
可设正方形ABCD的边长为x,
则DF=
 ,OF=x-2,
,OF=x-2,∴在直角△OFD中,(x-2)2+
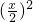 =52,
=52,解得x=6;
即正方形ABCD的边长为6.
故选B.
点评:本题主要考查了垂径定理及勾股定理的应用,本题结合已知构建直角△OFD,是解答的关键,解决问题时,要善于把问题与数学中的理论知识联系起来.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
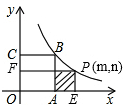 .并设阴影部分为S.
.并设阴影部分为S. 的图象上,点P(m,n)是函数
的图象上,点P(m,n)是函数 (k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S.
(k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S. 时,求点P的坐标.
时,求点P的坐标.
 的图象上,点P(m,n)是函数
的图象上,点P(m,n)是函数 (k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S.
(k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S. 时,求点P的坐标.
时,求点P的坐标.
 的图象上,点P(m,n)是函数
的图象上,点P(m,n)是函数 (k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S.
(k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S. 时,求点P的坐标.
时,求点P的坐标.
 的图象上,点P(m,n)是函数
的图象上,点P(m,n)是函数 (k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S.
(k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S. 时,求点P的坐标.
时,求点P的坐标.