题目内容
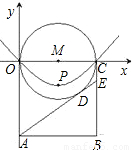
如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数y= 的图象上,点P(m,n)是函数
的图象上,点P(m,n)是函数 (k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S.
(k>0,x>0)的图象上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设阴影部分为S.(1)求B点坐标和k的值;
(2)求S关于m的函数关系式;
(3)当S=
 时,求点P的坐标.
时,求点P的坐标.
【答案】分析:(1)由于点B在函数y= 的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
(2)分类讨论阴影部分(矩形)的面积;
(3)根据(2)函数关系式即可求解.
解答:解:(1)∵正方形OABC的面积为9,
∴正方形OABC的边长为3,即OA=3,AB=3,
∴B点坐标为(3,3).
又∵点B是函数 的图象上的一点,
的图象上的一点,
∴ ,
,
∴k=9;
(2)分两种情况:
若点P在点B的右侧,如图(1),
 则PE=n,AE=m-3,
则PE=n,AE=m-3,
∴S= ;
;
若点P在点B的左侧,如图(2),
则PF=m,FC=n-3,
∴S= ;
;
(3)若点P在点B的右侧,
由(2)有 ,
,
∴m=6,
∴ ,
,
∴P ;
;
若点P在点B的左侧,
由(2)有 ,
,
解得 ,
,
∴ ,
,
∴P ,
,
∴点P的坐标是 或
或 (12分)
(12分)
点评:此题解题关键是利用了分类讨论的数学思想,能够培养学生严谨的思维习惯.此题主要考查了反比例函数的图象和性质.
 的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;(2)分类讨论阴影部分(矩形)的面积;
(3)根据(2)函数关系式即可求解.
解答:解:(1)∵正方形OABC的面积为9,
∴正方形OABC的边长为3,即OA=3,AB=3,
∴B点坐标为(3,3).
又∵点B是函数
 的图象上的一点,
的图象上的一点,∴
 ,
,∴k=9;
(2)分两种情况:
若点P在点B的右侧,如图(1),
 则PE=n,AE=m-3,
则PE=n,AE=m-3,∴S=
 ;
;若点P在点B的左侧,如图(2),
则PF=m,FC=n-3,
∴S=
 ;
;(3)若点P在点B的右侧,
由(2)有
 ,
,∴m=6,
∴
 ,
,∴P
 ;
;若点P在点B的左侧,
由(2)有
 ,
,解得
 ,
,∴
 ,
,∴P
 ,
,∴点P的坐标是
 或
或 (12分)
(12分)点评:此题解题关键是利用了分类讨论的数学思想,能够培养学生严谨的思维习惯.此题主要考查了反比例函数的图象和性质.

练习册系列答案
相关题目
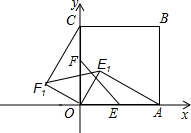 2.将三角板OEF绕O点逆时针旋转至OE1F1的位置,连接CF1、AE1.
2.将三角板OEF绕O点逆时针旋转至OE1F1的位置,连接CF1、AE1.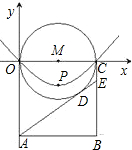 立平面直角坐标系,使点B落在第四象限,一条抛物线y=ax2+bx经过O、C两点,并将抛物线的顶点记作P.
立平面直角坐标系,使点B落在第四象限,一条抛物线y=ax2+bx经过O、C两点,并将抛物线的顶点记作P. 如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=
如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=