题目内容
8. 如图,已知抛物线y=ax2+bx-3与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C,其顶点为D,对称轴为直线x=1.
如图,已知抛物线y=ax2+bx-3与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C,其顶点为D,对称轴为直线x=1.(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ACM是以AC为一腰的等腰三角形时,求点M的坐标.
分析 (1)利用对称性可得B(3,0),则利用交点式得抛物线解析式为y=a(x+1)(x-3)=ax2-2ax-3a,所以-3a=3,解得a=1,于是得到抛物线解析式为y=x2-2x-3;
(2)分类讨论:当AC=AM时,易得点M1(0,3),如图;②当CM=CA时,先计算出AC=$\sqrt{10}$,再以C点为圆心,CA为半径画弧交y轴于M2,M3,如图,易得M2(0,$\sqrt{10}$-3),M3(0,-$\sqrt{10}$-3).
解答 解:(1)∵点A(-1,0)和点B关于直线x=1对称,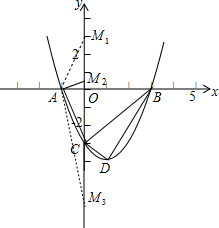
∴B(3,0),
∴抛物线解析式为y=a(x+1)(x-3)=ax2-2ax-3a,
∴-3a=3,解得a=1,
∴抛物线解析式为y=x2-2x-3;
(2)当AC=AM时,点M1与点C关于x轴对称,则M1(0,3),如图;
②当CM=CA时,AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
以C点为圆心,CA为半径画弧交y轴于M2,M3,如图,则OM2=$\sqrt{10}$-1,OM3=OC+CM3=3+$\sqrt{10}$,则M2(0,$\sqrt{10}$-3),M3(0,-$\sqrt{10}$-3).
综上所述,满足条件的点M的坐标为(0,3),(0,$\sqrt{10}$-3),(0,-$\sqrt{10}$-3).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决(2)小题的关键是利用等腰三角形的性质画出点M的坐标.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
18.下列实数中,无理数是( )
| A. | -$\frac{2}{7}$ | B. | 0 | C. | 3.14159 | D. | $\frac{\sqrt{21}}{3}$ |
19.土家传统建筑的窗户上常有一些精致花纹,小辰对土家传统建筑非常感兴趣,他观察发现窗格的花纹排列呈现有一定规律,如图.其中“O”代表的就是精致的花纹,请问有35个精致花纹的是第( )个图.


| A. | 13 | B. | 11 | C. | 9 | D. | 7 |
3.下列各式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{{m}^{5}}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{6}$ |
13.下表是同一时刻4个城市的国际标准时间,那么北京与多伦多的时差为12 h.
| 城市 | 伦敦 | 北京 | 东京 | 多伦多 |
| 国际标准时间 | 0 | +8 | +9 | -4 |
18.与3-$\sqrt{8}$乘积结果不含根号的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{2}$ | C. | 3$+\sqrt{8}$ | D. | 3$-\sqrt{8}$ |
 如图,在平面直角坐标系中,⊙P经过点A(0,$\sqrt{3}$)、O(0,0)、B(1,0),点C在第一象限的$\widehat{AB}$上,则∠BCO的度数为30°.
如图,在平面直角坐标系中,⊙P经过点A(0,$\sqrt{3}$)、O(0,0)、B(1,0),点C在第一象限的$\widehat{AB}$上,则∠BCO的度数为30°.