题目内容
在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f,
(1)当m、n互质(m、n除1外无其他公因数)时,观察下列图形并完成下表:
|
|
|
|
1 | 2 | 3 | 2 |
1 | 3 | 4 | 3 |
2 | 3 | 5 | 4 |
2 | 4 | 7 | |
3 | 5 | 7 |

猜想:当m、n互质时,在m×n的矩形网格中,一条对角线所穿过的小正方形的个数f与m、n的关系式是______________________________(不需要证明);
2)当m、n不互质时,请画图验证你猜想的关系式是否依然成立,
解析:(1)通过题中所给网格图形,先计算出2×5,3×4,对角线所穿过的小正方形个数f,再对照表中数值归纳f与m、n的关系式.
(2)根据题意,画出当m、n不互质时,结论不成立的反例即可.
解:(1)如表:
|
|
|
|
1 | 2 | 3 | 2 |
1 | 3 | 4 | 3 |
2 | 3 | 5 | 4 |
2 | 4 | 7 | 6 |
3 | 5 | 7 | 6 |
f=m+n-1
(2)当m、n不互质时,上述结论不成立,如图2×4

2×4

练习册系列答案
相关题目

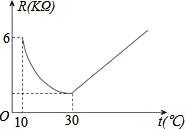 升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加
升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加

 如图,在由边为1的小正方形组成的网格中,将△ABC平移到△A′B′C′的位置,其中点C的对应点为C′,
如图,在由边为1的小正方形组成的网格中,将△ABC平移到△A′B′C′的位置,其中点C的对应点为C′,