题目内容
15.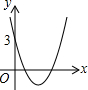 已知二次函数y=x2+bx+3如图所示,那么函数y=x2+(b-1)x+3的图象可能是( )
已知二次函数y=x2+bx+3如图所示,那么函数y=x2+(b-1)x+3的图象可能是( )| A. | 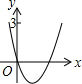 | B. | 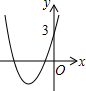 | C. |  | D. | 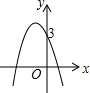 |
分析 根据函数y=x2+(b-1)x+3可知该函数的开口方向和一定过点(0,3),且通过变形可以与二次函数y=x2+bx+3建立关系,从而可以解答本题.
解答 解:∵函数y=x2+(b-1)x+3的a=1>0,过点(0,3),
∴该函数的图象开口向上,一定过点(0,3),
故选项A、D错误;
又∵二次函数y=x2+bx+3的图象已知,对称轴在y轴右侧,故可知b<0,所以b-1<0,
抛物线y=x2+(b-1)x+3的对称轴为x=$-\frac{b-1}{2}$>0,即对称轴也在y轴的右侧,
故选项B错误,选项C正确,
故选C.
点评 本题考查二次函数的图象,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
3.下列各组长度线段能组成三角形的是( )
| A. | 1cm,3cm,5cm | B. | 1cm,1cm,2cm | C. | 1cm,2cm,3cm | D. | 1cm,2cm,2cm |
10. 如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是( )
如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是( )
 如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是( )
如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是( )| A. | SSS | B. | SAS | C. | AAS | D. | HL |
7.(-a3)2的计算结果是( )
| A. | a2•a3 | B. | a6 | C. | -a5 | D. | -a6 |
 ,其中
,其中 .
. 如图,在△ABC中,∠B=15°,∠C=60°,AC=2,求BC长度.(tan15°=2-$\sqrt{3}$)
如图,在△ABC中,∠B=15°,∠C=60°,AC=2,求BC长度.(tan15°=2-$\sqrt{3}$)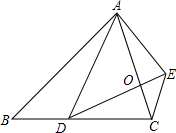 已知:如图,已知△ABC与△ADE均为等腰三角形,BA=BC,DA=DE.如果点D在BC边上,且∠EDC=∠BAD.点O为AC与DE的交点.
已知:如图,已知△ABC与△ADE均为等腰三角形,BA=BC,DA=DE.如果点D在BC边上,且∠EDC=∠BAD.点O为AC与DE的交点.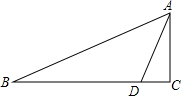 “学数学”最终是为了“用数学”,我市纪台一中校园内有一文物古迹-古纪国点将台,九年级数学兴趣小组想用所学知识测量出点将台的现在高度,操作方案如下:在地面B处测得其顶部A的仰角为30°,自B处沿BC方向进行14m到D点,又测得其顶部A的仰角为60°,你能算出点将台的高度吗?(结果保留两位小数)
“学数学”最终是为了“用数学”,我市纪台一中校园内有一文物古迹-古纪国点将台,九年级数学兴趣小组想用所学知识测量出点将台的现在高度,操作方案如下:在地面B处测得其顶部A的仰角为30°,自B处沿BC方向进行14m到D点,又测得其顶部A的仰角为60°,你能算出点将台的高度吗?(结果保留两位小数)