题目内容
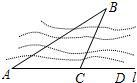 如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )米.
如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )米.| A、25 | ||||
B、25
| ||||
C、
| ||||
D、25+25
|
分析:过点B作BE⊥AD于E,设BD=x,则可以表示出CE,AE的长,再根据已知列方程从而可求得BD的长.
解答: 解:过点B作BE⊥AD于E.
解:过点B作BE⊥AD于E.
设BE=x.
∵∠BCD=60°,tan∠BCE=
,
∴CE=
x.
在直角△ABE中,AE=
x,AC=50米,
则
x-
x=50.
解得x=25
.
即小岛B到公路l的距离为25
米.
故选B.
 解:过点B作BE⊥AD于E.
解:过点B作BE⊥AD于E.设BE=x.
∵∠BCD=60°,tan∠BCE=
| BE |
| CE |
∴CE=
| ||
| 3 |
在直角△ABE中,AE=
| 3 |
则
| 3 |
| ||
| 3 |
解得x=25
| 3 |
即小岛B到公路l的距离为25
| 3 |
故选B.
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
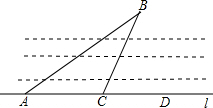 如图,小明要测量河内小岛B到河边公路L的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路L的距离为
如图,小明要测量河内小岛B到河边公路L的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路L的距离为 ,在C点测得
,在C点测得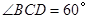 ,又测得
,又测得 米,则小岛B到公路l的距离为( )米.
米,则小岛B到公路l的距离为( )米.
 C.
C.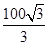 D.
D.
 ,在C点测得
,在C点测得 ,又测得
,又测得 米,则小岛B到公路l的距离为(
)米.
米,则小岛B到公路l的距离为(
)米.
 C.
C. D.
D.



