题目内容
如图,直线 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线 在第一象限交于B、C两点,且AB·AC=4,则k=_________.
在第一象限交于B、C两点,且AB·AC=4,则k=_________. 
 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线 在第一象限交于B、C两点,且AB·AC=4,则k=_________.
在第一象限交于B、C两点,且AB·AC=4,则k=_________. 

对直线方程 ,令y=0,得到x=
,令y=0,得到x= b,即直线与x轴的交点D的坐标为(
b,即直线与x轴的交点D的坐标为( b,0),令x=0,得到y=b,即A点坐标为(0,b),∴OA=b,OD=
b,0),令x=0,得到y=b,即A点坐标为(0,b),∴OA=b,OD= b,
b,
∵在Rt△AOD中,tan∠ADO= ,
,
∴∠ADO=30°,即直线y=- +b与x轴的夹角为30°,
+b与x轴的夹角为30°,
∵直线y=- x+b与双曲线
x+b与双曲线 在第一象限交于点B、C两点,
在第一象限交于点B、C两点,
∴- x+b=
x+b= ,即-
,即- x2+bx-k=0,
x2+bx-k=0,
由韦达定理得:x1x2= =
= k,即EB•FC=
k,即EB•FC= k,
k,
∵ =cos30°=
=cos30°= ,∴AB=
,∴AB= EB,同理可得:AC=
EB,同理可得:AC= FC,
FC,
∴AB•AC=( EB)(
EB)( FC)=
FC)= EB•FC=
EB•FC= k=4,解得:k=
k=4,解得:k= .
.

 ,令y=0,得到x=
,令y=0,得到x= b,即直线与x轴的交点D的坐标为(
b,即直线与x轴的交点D的坐标为( b,0),令x=0,得到y=b,即A点坐标为(0,b),∴OA=b,OD=
b,0),令x=0,得到y=b,即A点坐标为(0,b),∴OA=b,OD= b,
b,∵在Rt△AOD中,tan∠ADO=
 ,
,∴∠ADO=30°,即直线y=-
 +b与x轴的夹角为30°,
+b与x轴的夹角为30°,∵直线y=-
 x+b与双曲线
x+b与双曲线 在第一象限交于点B、C两点,
在第一象限交于点B、C两点,∴-
 x+b=
x+b= ,即-
,即- x2+bx-k=0,
x2+bx-k=0,由韦达定理得:x1x2=
 =
= k,即EB•FC=
k,即EB•FC= k,
k,∵
 =cos30°=
=cos30°= ,∴AB=
,∴AB= EB,同理可得:AC=
EB,同理可得:AC= FC,
FC,∴AB•AC=(
 EB)(
EB)( FC)=
FC)= EB•FC=
EB•FC= k=4,解得:k=
k=4,解得:k= .
.

练习册系列答案
相关题目
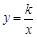 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.  的图象与
的图象与 轴、
轴、 轴分别交于A、B两点且与反比例函数
轴分别交于A、B两点且与反比例函数 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥ ,A B =
,A B =  ,C D =
,C D = 


 的图象在各个象限内
的图象在各个象限内 随着
随着 的增大而增大,则
的增大而增大,则 的取值范围是( ▲ )
的取值范围是( ▲ )



 的图象,观察图象写出y1>y2时,
的图象,观察图象写出y1>y2时, 的取值范围 .
的取值范围 .
 的图象经过点A(m,1),则m的值为 ▲ .
的图象经过点A(m,1),则m的值为 ▲ . 的图像上有两点
的图像上有两点 ,
, ,若 0﹤
,若 0﹤ ﹤
﹤ ,则
,则  ﹤
﹤
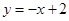 与
与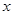 轴、
轴、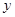 轴分别交于
轴分别交于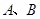 两点,过
两点,过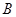 点作
点作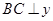 轴与双曲线
轴与双曲线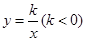 交于
交于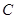 点,过
点,过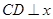 轴于
轴于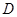 .若梯形
.若梯形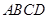 的面积为4,则
的面积为4,则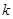 的值为_____.
的值为_____.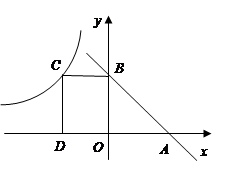
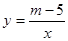 ,当
,当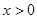 时,其图象位于第一象限,则m的取值范围是 ,此时
时,其图象位于第一象限,则m的取值范围是 ,此时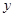 随
随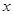 的增大而 。
的增大而 。