Question

如图，直线y=-

3

3

x+1与x轴、y轴分别交于A、B，以线段AB为直角边在第一象限内作等腰直角△ABC，∠BAC=90°．在第二象限内有一点P(a，

1

2

)，且△ABP的面积与△ABC的面积相等．则△ABC的面积是

 

；a=

 

．

Answer 1

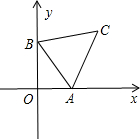
分析：根据题意，易得A、B点的坐标，可得AB的长，又有△ABC是等腰直角三角形，进而可得△ABC的面积，已知△ABP的面积与△ABC的面积相等，即P到直线AB的距离与AC长度相等，列出关系式可得P的坐标，进而可得a的值．

解答：解：根据题意，直线y=-

3

3

x+1与x轴、y轴分别交于A、B，
则A（

3

，0），B（0，1），
即OA=

3

，OB=1，则AB=2；
又有△ABC是等腰直角三角形，即AB=AC=2，∠BAC=90°，
则S_△ABC=

1

2

×AB×AC=2；
同时又有△ABP的面积与△ABC的面积相等，
则即P到直线AB的距离与AC长度相等，即到AB的距离为2，
可得：|

3 3 ×a+ 1 2 -1

( 3 3 )2+1

|=2，
解可得|

3 a- 3 2

2 3

|=2，
∴

3 a- 3 2

2 3

=2或

3 a- 3 2

2 3

=-2，

解得：a=

3

2

±4，P在第二象限，
故a=

3

2

-4；
故答案为2，

3

2

-4．

点评：本题有一定难度，需要认真分析题意，结合两点间的距离、点到直线的距离进行解题．