Question

【题目】如图，山顶有一塔，塔高．计划在塔的正下方沿直线开通穿山隧道．从与点相距的处测得、的仰角分别为、，从与点相距的处测得的仰角为．求隧道的长度．（参考数据：，．）

Answer 1

【答案】

【解析】

延长AB交CD于H，利用正切的定义用CH表示出AH、BH，根据题意列式求出CH，计算即可．

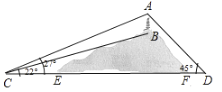
解：延长AB交CD于H，

则AH⊥CD，

在Rt△AHD中，∠D=45°， ∴AH=DH，

在Rt△AHC中，tan∠ACH=，

∴AH=CHtan∠ACH≈0.51CH，

在Rt△BHC中，tan∠BCH=，

∴BH=CHtan∠BCH≈0.4CH，

由题意得，0.51CH-0.4CH=33，

解得，CH=300，

∴DH=AH=153，

∴EH=CH-CE=220，

∴HF=DH-DF=103，

∴EF=EH+FH=323，

答：隧道EF的长度为323m．