Question

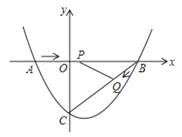
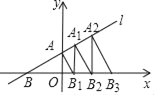
【题目】如图，在平面直角坐标系中，直线l：y=x+1交x轴于点B，交y轴于点A，过点A作AB1⊥AB交x轴于点B1，过点B1作B1A1⊥x轴交直线l于点A2…依次作下去，则点Bn的横坐标为_____．

Answer 1

【答案】

【解析】

根据直线的位置和一次函数图像点的位置即可求出该题答案.

有直线l：y＝x＋1交x轴于点B，交y轴于点A，可得A（0，1），B（－，0），

∴tan∠ABO＝，即∠ABO＝30°，

∴BA＝2AO＝2，

又∵AB1⊥AB交x轴于点B1，AO＝1，

∴AB1＝ ，

∴RT△BAB1中，BB1＝ ；

由题可得BA2＝，

∴A2B3＝ ，

∴RT△BA2B3中，BB3＝ ，

以此类推，BBn＝（）n，

又∵BO＝，

∴OBn＝（）n－，

∴点Bn的横坐标为（）n－，

故答案为：（）n－.