题目内容
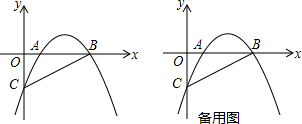
8.如图,抛物线y=ax2+$\frac{5}{2}x-2$与x轴相交于点A(1,0)与点B,与y轴相交于点C.(1)确定抛物线的解析式;
(2)连接AC、BC,△AOC与△COB相似吗?并说明理由;
(3)点N在抛物线的对称轴上,在抛物线上是否存在点M,使得以点N、M、A、B为顶点的四边形是平行四边形?若存在,求出对应的点M、N的坐标;若不存在,请说明理由.
分析 (1)直接把点A(1,0)代入抛物线的解析式求出a的值即可;
(2)求出A、B两点的坐标,再由$\frac{OA}{OC}$=$\frac{OC}{OB}$=$\frac{1}{2}$,∠COA=∠BOC可得出结论;
(3)分AB为平行四边形的对角线与AB为平行四边形的边两种情况进行讨论.
解答 解:(1)∵把A(1,0)代入得:a+$\frac{5}{2}$-2=0,解得a=-$\frac{1}{2}$,
∴y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2;
(2)相似.
∵令-$\frac{1}{2}$x2+$\frac{5}{2}$x-2=0,解得x1=1,x2=4,
∴A(1,0),B(4,0).
∵x=0时,y=-2,
∴C(0,-2).
∴OC=2,OA=1,OB=4
∴$\frac{OA}{OC}$=$\frac{OC}{OB}$=$\frac{1}{2}$.
又∵∠COA=∠BOC=90°,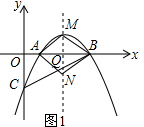 ∴△AOC∽△COB;
∴△AOC∽△COB;
(3)存在.
对称轴为x=$\frac{5}{2}$,交x轴于点Q,顶点坐标为($\frac{5}{2}$,$\frac{9}{8}$).
①如图1,AB为对角线,若四边形AMBN为平行四边形,
则QM=QN,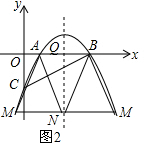 ∴M($\frac{5}{2}$,$\frac{9}{8}$),N($\frac{5}{2}$,-$\frac{9}{8}$);
∴M($\frac{5}{2}$,$\frac{9}{8}$),N($\frac{5}{2}$,-$\frac{9}{8}$);
②如图2,AB为一边,若四边形ABMN为平行四边形,则MN∥AB,MN=AB=3,
设N(2.5,n)则有M(-0.5,n)或(5.5,n)
将M坐标代入解析式:n=-$\frac{27}{8}$.
综上所述,M($\frac{5}{2}$,$\frac{9}{8}$),N($\frac{5}{2}$,-$\frac{9}{8}$)或M(-$\frac{1}{2}$,-$\frac{27}{8}$),N($\frac{5}{2}$,-$\frac{27}{8}$)或M(5.5,-$\frac{27}{8}$),N($\frac{5}{2}$,-$\frac{27}{8}$).
点评 本题考查的是二次函数综合题,涉及到二次函数图象上点的坐标特点,平行四边形的判定与性质等知识,在解答(3)时要注意进行分类讨论.

| A. | y=x | B. | y=-x | C. | y=-x2 | D. | y=x2-2 |
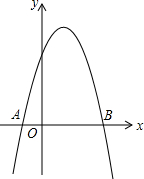 如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0).
如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0).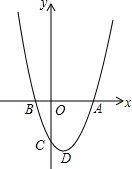 如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D. 由8个大小相同的正方体组成一个几何体,如图是分别从正面看和从上面看到的图形,则这个几何体从左面看到的图形是( )
由8个大小相同的正方体组成一个几何体,如图是分别从正面看和从上面看到的图形,则这个几何体从左面看到的图形是( )


