题目内容
如图，△ABC中，BE⊥AC，CF⊥AB，连接EF，求证：∠AFE=∠ACB．考点：相似三角形的判定与性质
专题：证明题
分析：可证△AEB∽△AFC，根据对应边比值相等可以判定△AFE∽△ACB，即可解题．
解答：证明：∵BE⊥AC，CF⊥AB，∠A=∠A，
∴△AEB∽△AFC，
∴
=
，即
=
，
∵∠A=∠A，
∴△AFE∽△ACB，
∴∠AFE=∠ACB．
∴△AEB∽△AFC，
∴
| AF |
| AE |
| AC |
| AB |
| AF |
| AC |
| AE |
| AB |
∵∠A=∠A，
∴△AFE∽△ACB，
∴∠AFE=∠ACB．
点评：本题考查了相似三角形对应边比例相等的性质，考查了相似三角形的判定．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
如图，AB∥CD，∠ACB=∠BDC=90°，CE⊥AB于点E，DF⊥CB于点F．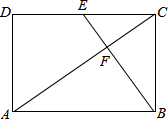
如图，矩形ABCD中，BE⊥AC于F，E恰是CD的中点，请问BF和AF之间存在怎样的数量关系？并请证明．
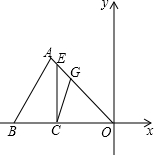如图，点B、点C都在x轴上，其中点B（-30，0）、C（-20，0），A在第二象限中，△ABO中，∠ABO=45°，∠AOB=30°，过点C作x轴的垂线，与AO交于点E．
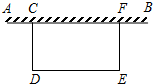如图，某校广场有一段25米差个的旧围栏，现打算利用该围栏的一部分（或全部）为一边，围成一块100平方米的长方形草坪（如图CDEF，CD＜CF）已知整修旧围栏的价格是每米1.75元，建新围栏的价格是4.5元．若CF=x米，计划修建费为y元．