Question

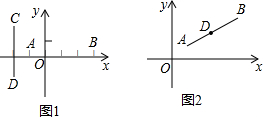
(1)在图1中，已知∠MAN＝120°，AC平分∠MAN．∠ABC＝∠ADC＝90°，则能得如下两个结论：① DC = BC; ②AD+AB=AC.请你证明结论②；

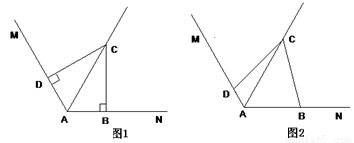
 (2)在图2中，把（1）中的条件“∠ABC＝∠ADC＝90°”改为∠ABC＋∠ADC＝180°，其他条件不变，则(1)中的结论是否仍然成立？若成立，请给出证明;若不成立，请说明理由．

 

Answer 1

【答案】

(1)证明见解析(2) 成立，证明见解析

【解析】（1）证明： ∵∠MAN＝120°，AC平分∠MAN．

                        ∴∠DAC = ∠BAC =60⁰

                        ∵∠ABC＝∠ADC＝90°，

                         ∴∠DCA＝∠BCA＝30°，                               

                        在Rt△ACD，Rt△ACB中，∠DCA＝30°

∠BCA＝30°

                        ∴AC=2AD，   AC = 2AB，

∴2AD=2AB    

∴AD=AB 

                         ∴AD+AB=AC.

（2）解：（1）中的结论① DC = BC; ②AD+AB=AC都成立，　　　　　　　

理由一：如图2，在AN上截取AE=AC，连结CE，                 

∵∠BAC =60°，

∴△CAE为等边三角形，

∴AC=CE，∠AEC =60°，                                             

∵∠DAC =60°，∴∠DAC =∠AEC，                                               

∵∠ABC＋∠ADC＝180°，∠ABC＋∠EBC＝180°，

∴∠ADC =∠EBC， ∴，                                                                                                                                                                              

∴DC = BC，DA = BE，  …

∴AD+AB=AB+BE=AE，   ∴AD+AB=AC．

或者理由二：如图，过C作CE⊥AN,CF⊥AM于E、F

证明△BCE≌△DCF,得到

DC=BC,BE=DF

即AC=AE+AF=AB+AD亦可

得分参照理由一给分

（1）根据角平分线的性质可得∠DAC=∠BAC=60°，又已知∠ABC=∠ADC=90°，所以∠DCA=∠BCA=30°，根据直角三角形的性质可证AC=2AD，AC=2AB，所以AD+AB=AC．

（2）根据已知条件可在AN上截取AE=AC，连接CE，根据AAS可证△ADC≌△EBC，得到DC=BC，DA=BE，所以AD+AB=AB+BE=AE，即AD+AB=AC．