题目内容
如图所示,在□ABCD中,对角线AC,BD相交于点O,下列条件能判定□ABCD为菱形的是( ).
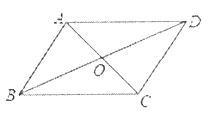
A. ∠ABC=90° B. AC=BD
C. AC⊥BD D. OA=OC,OB=OD
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
题目内容
如图所示,在□ABCD中,对角线AC,BD相交于点O,下列条件能判定□ABCD为菱形的是( ).

A. ∠ABC=90° B. AC=BD
C. AC⊥BD D. OA=OC,OB=OD
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案