题目内容
一个四位数的首位数字是7,如果将首位上的数字移到个位数字的右边,变成一个新的四位数,那么所得到的新四位数比原四位数的一半多3,求原四位数.
考点:一元一次方程的应用
专题:
分析:设7后面的三位数是x,则新的四位数是10x+7.依据“新四位数比原四位数的一半多3”列出方程并求解即可.
解答:解:设7后面的三位数是x,则新的四位数是10x+7.则
10x+7=
(7000+x)+3,
解得 x=368.
则原来的四位数是7368.
答:原来的四位数是7368.
10x+7=
| 1 |
| 2 |
解得 x=368.
则原来的四位数是7368.
答:原来的四位数是7368.
点评:本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
如果方程5x+5y-2+3kx-2ky-5k=0(k为常数)是关于x的一元一次方程,那么k的值应该是( )
| A、0 | ||
B、
| ||
C、-
| ||
D、
|
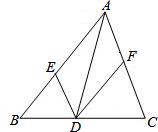 已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F.
已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F.