题目内容
半径为1的圆内接正三角形的边心距为 .

 .
.
【考点】正多边形和圆.
【专题】几何图形问题.
【分析】作出几何图形,再由外接圆半径、边心距和边长的一半组成的三角形中,已知外接圆半径和特殊角,可求得边心距.
【解答】解:如图,△ABC是⊙O的内接等边三角形,OB=1,OD⊥BC.
∵等边三角形的内心和外心重合,
∴OB平分∠ABC,则∠OBD=30°;
∵OD⊥BC,OB=1,
∴OD=
 .
.
故答案为:
 .
.


【点评】考查了等边三角形的性质.注意:等边三角形的外接圆和内切圆是同心圆,圆心到顶点的距离等于外接圆半径,边心距等于内切圆半径.

练习册系列答案
相关题目
 ABCD中,AD=5cm,AB⊥BD,点O是两条对角线的交点,OD=2 cm,则AB=______cm.
ABCD中,AD=5cm,AB⊥BD,点O是两条对角线的交点,OD=2 cm,则AB=______cm.
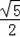
 ,如果Rt△ABC的面积为1,则它的周长为( )
,如果Rt△ABC的面积为1,则它的周长为( )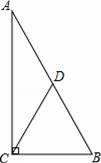

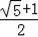
 B.
B.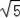
 +1 C.
+1 C.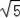

 ,y=
,y=
 ,求
,求
 的值.
的值.