题目内容
已知：在Rt△ABC，∠C=90°，D是BC边的中点，DE⊥AB于E，tanB=| 1 | 2 |
分析：首先表示出BD的长，进而得出AB=5x，由AB=AE+BE，得出5x=7+2x，求出x即可．
解答：解：∵DE⊥AB于E，
∴tanB=
=
，
设DE=x，
∴BE=2x，
∴BD=
=
x，
∴cosB=
=
，
∵∠C=90°，∴cosB=
=
=
，
∵D是BC边的中点，∴BC=2BD=2
x，
∴AB=
BC=5x，
∵AE=7，
∴AB=AE+BE，
5x=7+2x，
x=
．
故DE=
．
∴tanB=
| DE |
| BE |
| 1 |
| 2 |
设DE=x，
∴BE=2x，
∴BD=
| DE2+BE2 |
| 5 |
∴cosB=
| BE |
| BD |
| 2 | ||
|
∵∠C=90°，∴cosB=
| BC |
| AB |
| BE |
| BD |
| 2 | ||
|
∵D是BC边的中点，∴BC=2BD=2
| 5 |
∴AB=
| ||
| 2 |
∵AE=7，
∴AB=AE+BE，
5x=7+2x，
x=
| 7 |
| 3 |
故DE=
| 7 |
| 3 |
点评：此题主要考查了解直角三角形，关键是利用三角函数求出AB=5x，进而得出DE的长．
练习册系列答案
相关题目
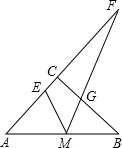如图，已知：在Rt△ABC中，∠ACB=90°，AC=BC=4，M是边AB的中点，E、G分别是边AC、BC上的一点，∠EMG=45°，AC与MG的延长线相交于点F．
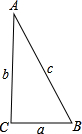已知：在Rt△ABC中，∠C=90°，∠A=30°，b=
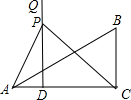重合），过D作DQ⊥AC（DQ与AB在AC的同侧）；点P从D点出发，在射线DQ上运动，连接PA、PC．
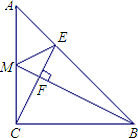已知：在Rt△ABC中，∠C=90°，AC=BC，M是AC的中点，连接BM，CF⊥MB，F是垂足，延长CF交AB于点E．求证：∠AME=∠CMB．
已知：在Rt△ABC中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC、AB分别交于点D、E，且∠CBD=∠A．