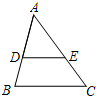题目内容
已知在△ABC中，BE平分∠ABC交AC于点E，ED∥CB交AB于点D，AB=4，BC=5，则BD的长为______．
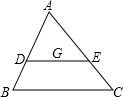
连接BE．
∵ED∥CB，
∴∠DEB=∠EBC，
∵BE平分∠ABC，
∴∠DBE=∠EBC，
∴∠DBE=∠BED，
∴BD=DE，
设BD=x，则DE=x，
∵AB=4，
∴AD=4-x，
∵ED∥CB，
∴
=
，
即：
=
，
解得：x=
．
∴BD=
．
故答案为：
．
∵ED∥CB，
∴∠DEB=∠EBC，
∵BE平分∠ABC，
∴∠DBE=∠EBC，
∴∠DBE=∠BED，
∴BD=DE，
设BD=x，则DE=x，
∵AB=4，
∴AD=4-x，
∵ED∥CB，
∴
| DE |
| BC |
| AD |
| AB |
即：
| x |
| 5 |
| 4-x |
| 4 |
解得：x=
| 20 |
| 9 |
∴BD=
| 20 |
| 9 |
故答案为：
| 20 |
| 9 |
练习册系列答案
相关题目
．
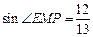、E分别与△ENB的顶点E、N、B对应），求AP的
长．
