题目内容
如图，BC⊥AE，垂足为C，CD平分∠ECB，CD∥AB．则∠B=________．
45°
分析：求出∠BCE=90°，求出∠DCB=
∠BCE=45°，根据平行线性质得出∠B=∠BCD，代入求出即可．
解答：∵BC⊥AE，
∴∠BCE=90°，
∵CD平分∠ECB，
∴∠DCB=∠BCE=45°，
∵CD∥AB，
∴∠B=∠BCD=45°，
故答案为：45°．
点评：本题考查了平行线性质，角平分线定义，垂直定义的应用，关键是求出∠BCD的度数．
分析：求出∠BCE=90°，求出∠DCB=
∠BCE=45°，根据平行线性质得出∠B=∠BCD，代入求出即可．解答：∵BC⊥AE，
∴∠BCE=90°，
∵CD平分∠ECB，
∴∠DCB=
∠BCE=45°，∵CD∥AB，
∴∠B=∠BCD=45°，
故答案为：45°．
点评：本题考查了平行线性质，角平分线定义，垂直定义的应用，关键是求出∠BCD的度数．
练习册系列答案
相关题目
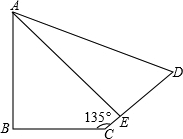如图，在四边形ABCD中，线段BC=6cm，∠ABC=90°，∠BCD=135°，而且点A到边CD的垂线段AE的长为12cm，线段ED的长为5cm，则四边形ABCD的面积=
如图，∠ABC=90°，AB=BC．
