题目内容
已知AB是半圆O的直径，AC是弦，以AC为直径作半圆P，与AB交于点D，∠B=55°，则∠CPD为考点：圆周角定理
专题：
分析：连结CD．先由半圆（或直径）所对的圆周角是直角，得出∠ACB=90°，∠ADC=90°，根据同角的余角相等得出∠ACD=∠B=55°，再由等边对等角得到∠PDC=∠PCD=55°，然后根据三角形内角和定理求出∠CPD=180°-∠PDC-∠PCD=70°．
解答：
解：如图，连结CD．
∵AB是半圆O的直径，
∴∠ACB=90°，
∵AC为半圆P的直径，
∴∠ADC=90°，
∴∠ACD=∠B=90°-∠BCD=55°，
∵PC=PD，
∴∠PDC=∠PCD=55°，
∴∠CPD=180°-∠PDC-∠PCD=70°．
故答案为70．
解：如图，连结CD．∵AB是半圆O的直径，
∴∠ACB=90°，
∵AC为半圆P的直径，
∴∠ADC=90°，
∴∠ACD=∠B=90°-∠BCD=55°，
∵PC=PD，
∴∠PDC=∠PCD=55°，
∴∠CPD=180°-∠PDC-∠PCD=70°．
故答案为70．
点评：本题考查了圆周角定理，余角的性质，等腰三角形的性质，三角形内角和定理，难度适中．求出∠PDC=∠PCD=55°是解题的关键．
练习册系列答案
相关题目
在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上运动，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．
如图，OB是∠AOC的平分线，OD是∠COE的平分线，如果∠AOE=140°，∠COD=30°，那么∠BOD是多少度？∠AOB是多少度？
如图四边形ABCD，以AB为边作△ABM，使S△ABM=S四边形ABCD．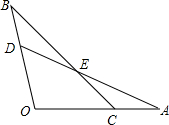
如图，OA=OB，∠A=∠B，有下列3个结论：①△AOD≌△BOC，②EA=EB，③点E在∠O的平分线上．④若OC=2CA，△AEC的面积为1，那么四边形OCED的面积为4．其中正确的结论个数为（ ）