题目内容
如图，EF是△ABC的中位线，将△AEF沿中线AD方向平移到△A1E1F1的位置，使E1F1与BC边重合，已知△AEF的面积为7，则图中阴影部分的面积为
- A.7
- B.14
- C.21
- D.28
B
分析：根据三角形的中位线定理，结合相似三角形的性质可以求得三角形ABC的面积，从而求解．
解答：∵EF是△ABC的中位线，
∴EF∥BC，EF=
BC．
∴△AEF∽△ACB．
∴
=
．
∴△ABC的面积=28．
∴图中阴影部分的面积为28-7-7=14．
故选B．
点评：此题综合运用了三角形的中位线定理和相似三角形的判定和性质．
分析：根据三角形的中位线定理，结合相似三角形的性质可以求得三角形ABC的面积，从而求解．
解答：∵EF是△ABC的中位线，
∴EF∥BC，EF=
BC．∴△AEF∽△ACB．
∴
=．∴△ABC的面积=28．
∴图中阴影部分的面积为28-7-7=14．
故选B．
点评：此题综合运用了三角形的中位线定理和相似三角形的判定和性质．
练习册系列答案
相关题目
3、如图，EF是△ABC的中位线，则有EO：OC=（ ）
如图，EF是△ABC的中位线，将△AEF沿中线AD方向平移到△A1E1F1的位置，使E1F1与BC边重合，已知△AEF的面积为7，则图中阴影部分的面积为（ ）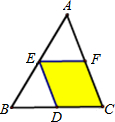
16、如图，EF是△ABC的中位线，将△AEF沿AB方向平移到△EBD的位置，点D在BC上，已知△AEF的面积为5，则图中阴影部分的面积为
如图，EF是△ABC的中位线，将△AEF沿中线AD的方向平移到△A1E1F1，使线段E1F1落在BC边上，若△AEF的面积为7cm2，则图中阴影部分的面积是