题目内容
【题目】已知![]() (本题中的角均大于
(本题中的角均大于![]() 且小于
且小于![]() )
)
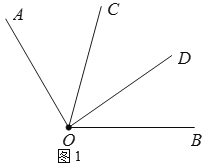
(1)如图1,在![]() 内部作
内部作![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
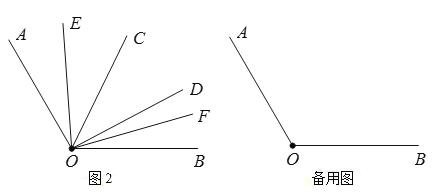
(2)如图2,在![]() 内部作
内部作![]() ,
,![]() 在
在![]() 内,
内,![]() 在
在![]() 内,且
内,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)射线![]() 从
从![]() 的位置出发绕点
的位置出发绕点![]() 顺时针以每秒
顺时针以每秒![]() 的速度旋转,时间为
的速度旋转,时间为![]() 秒(
秒(![]() 且
且![]() ).射线
).射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .若
.若![]() ,则
,则![]() 秒.
秒.
【答案】(1)40;(2)84;(3)7.5或15或45
【解析】
(1)利用角的和差进行计算便可;
(2)设![]() ,则
,则![]() ,
,![]() ,通过角的和差列出方程解答便可;
,通过角的和差列出方程解答便可;
(3)分情况讨论,确定∠MON在不同情况下的定值,再根据角的和差确定t的不同方程进行解答便可.
解:(1))∵∠AOD+∠BOC=∠AOC+∠COD+∠BOD+∠COD=∠AOB+∠COD
又∵∠AOD+∠BOC=160°且∠AOB=120°
∴![]()
![]()
![]()
(2)![]() ,
,![]()
![]() 设
设![]() ,则
,则![]() ,
,![]()
则![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)当OI在直线OA的上方时,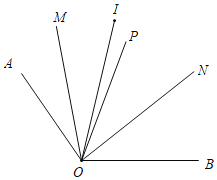
有∠MON=∠MOI+∠NOI=![]() (∠AOI+∠BOI))=
(∠AOI+∠BOI))=![]() ∠AOB=
∠AOB=![]() ×120°
×120°
∠PON=![]() ×60°=30°,
×60°=30°,
∵∠MOI=3∠POI,
∴3t=3(30-3t)或3t=3(3t-30),
解得t=![]() 或15;
或15;
当OI在直线AO的下方时,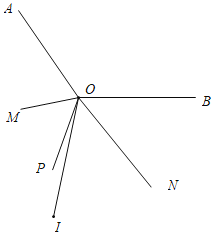
∠MON═![]() (360°-∠AOB)═
(360°-∠AOB)═![]() ×240°=120°,
×240°=120°,
∵∠MOI=3∠POI,
∴180°-3t=3(60°-![]() )或180°-3t=3(
)或180°-3t=3(![]() -60°),
-60°),
解得t=30或45,
综上所述,满足条件的t的值为![]() s或15s或30s或45s.
s或15s或30s或45s.

【题目】某农科所甲、乙试验田各有水稻3万个,为了考察水稻穗长的情况,于同一天在这两块试验田里分别随机抽取了![]() 个稻穗进行测量,获得了它们的长度
个稻穗进行测量,获得了它们的长度![]() (单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
(单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如下表所示(不完整):
甲试验田穗长频数分布表
分组/ | 频数 | 频率 |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
合计 | 50 | 1.00 |
b.乙试验田穗长的频数分布直方图如图所示:
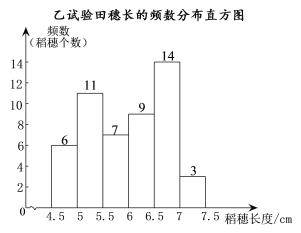
c.乙试验田穗长在![]() 这一组的是:
这一组的是:
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下(表2):
试验田 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 5.924 | 5.8 | 5.8 | 0.454 |
乙 | 5.924 |
| 6.5 | 0.608 |
根据以上信息,回答下列问题:
(1)表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)表中![]() 的值为 ;
的值为 ;
(3)在此次考察中,稻穗生长(长度)较稳定的试验田是 ;
A.甲 B.乙 C.无法推断
(4)若穗长在![]() 范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.