题目内容
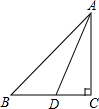 如图所示,已知:Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线.
如图所示,已知:Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线.求证:AC+CD=AB.
分析:过D作DE⊥AB于E,根据角平分线性质求出DE=DC,根据勾股定理求出AE=AC,求出∠B=45°,求出∠EDB=∠=45°,推出DE=BE=DC,代入即可求出答案.
解答:证明: 过D作DE⊥AB于E,
过D作DE⊥AB于E,
∵∠C=90°,
∴DC⊥AC,
∵AD是∠A的平分线,
∴DE=DC,
由勾股定理得:AE2=AD2-DE2,AC2=AD2-DC2,
∵AD=AD,DE=DC,
∴AE=AC,
∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠EDB=45°=∠B,
∴BE=DE=DC,
∴AB=AE+BE=AC+CD,
即AC+CD=AB.
 过D作DE⊥AB于E,
过D作DE⊥AB于E,∵∠C=90°,
∴DC⊥AC,
∵AD是∠A的平分线,
∴DE=DC,
由勾股定理得:AE2=AD2-DE2,AC2=AD2-DC2,
∵AD=AD,DE=DC,
∴AE=AC,
∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠EDB=45°=∠B,
∴BE=DE=DC,
∴AB=AE+BE=AC+CD,
即AC+CD=AB.
点评:本题考查了直角三角形,等腰三角形的性质和判定,角平分线性质,勾股定理等知识点的综合运用,关键是正确作辅助线后求出DE=BE=DC和AE=AC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
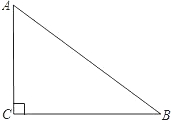 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°.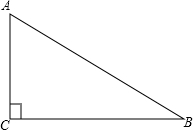 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°.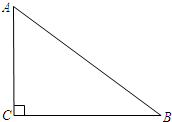 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°. 如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.
如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.