题目内容
在△ABC和△DEF中，∠C=∠F=90°．有如下五张背面完全相同的纸牌①、②、③、④、⑤，其正面分别写有五个不同的等式，小民将这五张纸牌背面朝上洗匀后先随机摸出一张（不放回），再随机摸出一张．请结合以上条件，解答下列问题．（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用①、②、③、④、⑤表示）；
（2）用两次摸牌的结果和∠C=∠F=90°作为条件，求能满足△ABC和△DEF全等的概率．
【答案】分析：（1）两两组合，列出表格将所有可能一一列举出来即可；
（2）利用全等三角形的判定将所有能组成全等三角形的条件列举出来，求得概率即可．
解答：解：（1）列表如下；
∴两次摸牌所有可能出现的结果共有20种
（用树状图解参照给分）
（2）两次摸牌所有可能出现的结果共有20种，其中满足△ABC≌△DEF的有18种可能，
∴P（能满足△ABC≌△DEF）=
点评：本题考查了列表法和树状图法求概率及全等三角形的判定．树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
（2）利用全等三角形的判定将所有能组成全等三角形的条件列举出来，求得概率即可．
解答：解：（1）列表如下；
| ① | ② | ③ | ④ | ⑤ | |
| ① | ①② | ①③ | ①④ | ①⑤ | |
| ② | ②① | ②③ | ②④ | ②⑤ | |
| ③ | ③① | ③② | ③④ | ③⑤ | |
| ④ | ④① | ④② | ④③ | ④⑤ | |
| ⑤ | ⑤① | ⑤② | ⑤③ | ⑤④ |
（用树状图解参照给分）
（2）两次摸牌所有可能出现的结果共有20种，其中满足△ABC≌△DEF的有18种可能，
∴P（能满足△ABC≌△DEF）=
点评：本题考查了列表法和树状图法求概率及全等三角形的判定．树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
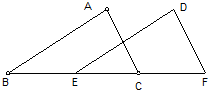20、如图，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件，请你在其中选3个作为条件，余下的1个作为结论，使其成为一个真命题，并加以证明．
如图所示，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有六个条件，请你在其中选三个作为已知条件，余下的选一个作为结论，编写出一个真命题，并说明理由．①AB=DE；②AC=DF；③∠ABC=∠DEF；④BE=CF；⑤∠ACB=∠DEF；⑥∠A=∠D（填写序号即可）
如图，已知BC∥EF，且BC=EF，AF=CD，则AB=DE，说明理由．