Question

4．如图，一座抛物线型拱桥，当水面宽AB为12m时，桥洞顶部离水面4m．若桥洞顶部离水面1m是警戒水位．求警戒水位时的水面宽度．

Answer 1

分析 以线段AB所在直线为x轴、AB的中垂线为y轴建立平面直角坐标系求出函数解析式，根据题意求出y=3时x的值即可的警戒水位时水面宽度．

解答 解：如图，以线段AB所在直线为x轴，AB的中垂线为y轴建立坐标系，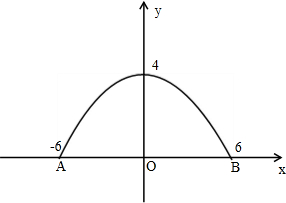

抛物线顶点（0，4）且经过（6，0），
设y=ax²+4，将点B（6，0）代入，得：36a+4=0，
∴$a=-\frac{1}{9}$，
∴$y=-\frac{1}{9}{x^2}+4$
当y=3时，$-\frac{1}{9}{x^2}+4=3$，解得：x=±3
故警戒水位时的水面宽度3-（-3）=6m．

点评 本题主要考查二次函数的实际应用能力，解决此问题首先建立合适的平面直角坐标系是解题的前提，熟练准确求出函数关系式是基本技能和关键．