Question

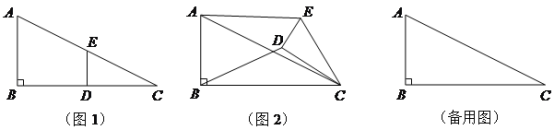
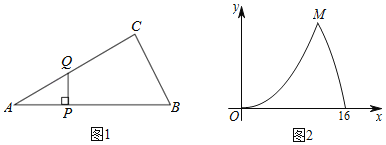
【题目】如图1，△ABC中，∠ACB＝90°，∠A＝30°，点P是斜边AB上一动点过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP＝x，△APQ的面积为y，图2是y关于x的函数图象，则图象上最高点M的坐标是_____．

Answer 1

【答案】（12，24）

【解析】

当点Q在线段AC上时，y＝AP×PQ＝x×x×tanA＝x2，当点Q在点C处时，即x＝ACcosA＝12，y为最大值，即可求解．

解：由图2知，AB＝16，

则BC＝8，AC＝，

则△ABC的高＝，

当点Q在线段AC上时，

y＝AP×PQ＝x×x×tanA＝x2，

当点Q在点C处时，即x＝ACcosA＝12，

y＝＝，为最大值，

即点M（4，8），

故答案为：（12，24）．