��Ŀ����
����Ŀ����֪��ͼ���ھ���ABCD�У�AB=6cm��BC=8cm���Խ���AC��BD���ڵ�0����P�ӵ�A��������AD�������յ�D�����˶����ٶ�Ϊ![]() cm/s��ͬʱ����Q�ӵ�D��������DC�������յ�C�����˶����ٶ�Ϊ1cm/s����һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶�������PO���ӳ�����BC�ڵ�E������Q��QF//AC����BD�ڵ�F�����˶�ʱ��Ϊt��s��������������⣺
cm/s��ͬʱ����Q�ӵ�D��������DC�������յ�C�����˶����ٶ�Ϊ1cm/s����һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶�������PO���ӳ�����BC�ڵ�E������Q��QF//AC����BD�ڵ�F�����˶�ʱ��Ϊt��s��������������⣺
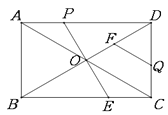
��1����tΪ��ֵʱ����AOP�ǵ��������Σ�
��2���������OECQF�����ΪS��cm2������ȷ��S��t�ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��t��ʹS�����S�����OECQF��S��ACD=9��16�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1) t=![]() ��t=5 (2) S=
��t=5 (2) S=![]() (3) t=3��t=
(3) t=3��t=![]()
��������
��1�������ݾ��ε����ʺ��ɶ����õ�AC=10cm���ٵ�AP=PO=t����P��PM��AO���Ӷ��õ�AM��֤����APM�ס�ACD���������������ε����ʵõ�AP=t��ֵ���ٸ�������ֱ�ӵõ��ڶ������������tֵ��
��2��������O��OH��BC��BC�ڵ�H�����ݾ��ε�����֤����DOP�ա�BOE���õ�BE=PD=8-t���Ӷ��õ���BOE�������
����FQ��AC��֤����DFQ�ס�DOC�������������ε�����ȿ������DFQ��������Ӷ����������OECQF�������
��3�����ɣ�2���ɵ������OECQF�����������S�����OECQF��S��ACD=9:16�з��̣��Է��̽�����⼴�ɵó�����.
��1�����ھ���ABCD�У�AB=6cm��BC=8cm��
��AC=10cm��
�ٵ�AP=PO=t����ͼ1��

��P��PM��AO��
��AM=![]() AO=
AO=![]() .
.
�ߡ�PMA=��ADC=90������PAM=��CAD��
���APM�ס�ACD��
��![]() ��
��
��AP=t=![]() ��
��
�ڵ�AP=AO=t=5ʱ����AOPΪ����������.
������������tΪ![]() ��5ʱ����AOP�ǵ���������.
��5ʱ����AOP�ǵ���������.
��2������O��OH��BC��BC�ڵ�H����OH=![]() CD=
CD=![]() AB=3cm��
AB=3cm��
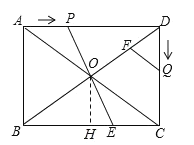
�ɾ��ε����ʿ�֪��PDO=��EBO��DO=BO���ֵá�DOP=��BOE��
���DOP�ա�BOE��
��BE=PD=8-t��
��S��BOE=![]() BE��OH=
BE��OH=![]() ��3��(8-t)=12-
��3��(8-t)=12-![]() t.
t.
��FQ��AC��
���DFQ�ס�DOC�����Ʊ�Ϊ![]() ��
��
��![]() ��
��
��S��DOC=![]() S����ABCD=
S����ABCD=![]() ��6��8=12
��6��8=12![]() ��
��
��S��DFQ=![]() =
=![]() ��
��
��S�����OECQF=S��DBC-S��BOE-S��DFQ=
![]() ��
��
��S��t�ĺ�����ϵʽΪS=![]() ��
��
��3������.
��S��ACD=![]() ��6��8=24��
��6��8=24��
��S�����OECQF��S��ACD=(![]() ):24=9:16��
):24=9:16��
���t=3��t=![]() ��
��
��t=3��![]() ʱ��S�����OECQF:S��ACD=9:16.
ʱ��S�����OECQF:S��ACD=9:16.

 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д�